Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 29
Resolva o Problema se o diâmetro da haste for . Use o método da área transformada discutido na Seção . , .
Passo 1
A uma viga de concreto sobre dois apoios simples possui uma haste que serve para aliviar a viga de qualquer tração.
Características da viga:
- Comprimento: .
- Largura: .
- Espessura: .
- Área transversal:
- Módulo de elasticidade da viga:
- Peso específico: .
- Diâmetro: .
- Área transversal:
- Posição do centro: a dos apoios (altura na seção) e no meio da seção transversal
Características da haste :
O peso da viga irá forçá-la para baixo. Queremos saber qual tração deve ter na haste para que na seção não tenhamos tração na viga!
A questão pede parar usarmos o “método da área transformada”. E realmente é uma boa, porque temos dois materiais no problema. Vamos começar calculando as propriedades da viga transformada.
Passo 2
Queremos trabalhar com uma viga equivalente, de um só material, para podermos usar nossas fórmulas de costume. Vamos transformar a área de aço em concreto. Calculamos o fator de transformação :
A área do aço transformado será
Essa área é pra ser considerada como feita de concreto! Afinal, transformamos de aço para concreto.
Beleza. Como a transformação aumenta a área , você pode imaginar que “enchemos” de concreto o buraco (haste ) e ainda sobrou um pouco mais de concreto. Devemos considerar essa sobra como concentrada (“achatada”) na mesma posição que estava a barra de aço: a dos apoios (altura), e o valor dela é
Tá, mas pra que estamos calculando isso? Porque com a transformação, mudou a área total e o mudou o segundo momento de área ! Precisamos desses caras para as fórmulas!
Passo 3
A área total após a transformação vai ser a viga inteira de concreto (“buraco” preenchido!) mais o excesso de concreto:
O segundo momento de área é um pouquinho mais complicado. Antes precisamos da posição do novo centroide . Faça por composição. Usando o topo da viga como referência, está na metade e está a (concentrada, lembre-se!):
Essa é a distância a partir do topo da viga! Com isso aí, podemos calcular . Usando o teorema dos eixos paralelos fica fácil, é só descontar a posição do centroide.
Ufa! Agora a questão volta ao natural dela. Podemos usar as fórmulas à vontaaaade!
Passo 4
Vamos ver uma seção da viga indo da extremidade na direita até a seção transversal .
O peso da viga atua no meio da seção. A intensidade vai ser o volume dessa seção (a área transversal vezes ) vezes o peso específico .
O diagrama de corpo livre vai nos mostrar como as forças agem.
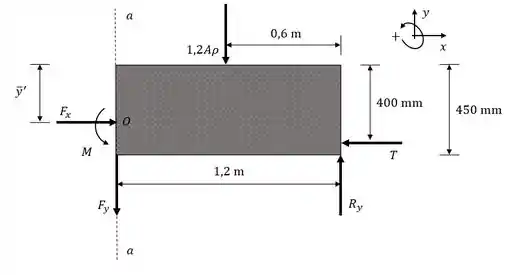
Queremos zerar a tração na direção . Dois efeitos causam essa tensão na seção : um devido a e outro devido a . Cuidado para não se confundir no sinal! Raciocine pensando nas direções que você assumiu no diagrama! Nessa figura, a compressão da seção tem sinal positivo e a tração tem sinal negativo .
- comprime .
- causa compressão para e tração para (eixo neutro no centro da viga).
O balanço da tensão na direção fica
A tração só vai ocorrer em . Para não ter tração, o valor máximo dela tem que ser cancelado pela compressão. O valor máximo de tração vai ocorrer topo da viga, que é o ponto mais distante do eixo neutro!
Fique atento que o eixo neutro não está no centro da viga! Ele está no centroide agora!
O balanço da tensão na direção fica
Beleza! Então precisamos descobrir quem é e , e achar o que isso tem a ver com a tração da haste .
Passo 5
Condições de equilíbrio! Olhe pra figura no Passo . Forças na horizontal:
Show! O que queremos já entrou na história!
O equilíbrio de forças na vertical não vai nos ajudar. Vamos ver o equilíbrio de momentos na seção , ao redor do ponto posicionado no eixo neutro (centroide):
Se calcularmos o , teremos o e o dependendo só de . É tudo que a gente quer!
Para achar é só lembrar que a reação vertical dos apoios tem que aguentar o peso da viga, e a reação em cada apoio é a mesma por causa da simetria. Fazendo o equilíbrio para a toda viga:
Voltando ao momento:
Agora só temos uma incógnita , só falta fazer umas continhas.
Passo 6
Voltando à equação que queremos forçar ser verdade, substitua , , e :
Resposta
Tração na haste :.