Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 199

A roda sola sem deslizar, e sua posição é controlada pelo movimento do cursor B. Se B possui uma velocidade constante de 250 mm/s para a esquerda, determine a velocidade angular de AB e a velocidade do centro O da roda quando θ = 0 .

Passo 1

Bom pessoal, vamos representar o mecanismo incluindo seus vetores velocidade no instante que θ = 0 .

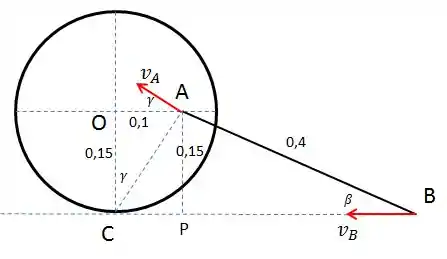
Beleza! Pelo triângulo AOC, podemos calcular o ângulo γ :

γ = tan - 1 ⁡ 0,1 0,15 = 33,69 °

Podemos ainda, calcular o ângulo β pelo triângulo APB:

β = s e n - 1 0,15 0,4 = 22 °

Como temos um problema de rolamento sem deslizamento, o ponto de contato C entre a roda e o chão é o centro instantâneo de velocidade nula. Desta forma, a velocidade de A está perpendicular à distância AB. Então podemos escrever v A em relação às direções x-y:

v A = v A ( - c o s γ   i ^ + s e n γ   j ^ )

Agora, a partir da haste AB, podemos usar a equação da velocidade relativa:

v A = v B + ω × r A B

v A - c o s γ   i ^ + s e n γ   j ^ = - 0,25 i ^ + ω k ^ × 0,4 ( - c o s β   i ^ + s e n β   j ^ )

v A - 0,832   i ^ + 0,555   j ^ = - 0,25 i ^ - 0,371 ω   j ^ - 0,15 ω   i ^

Decompondo nas direções, temos o sistema:

v A - 0,832   i ^ = - 0,25 i ^ - 0,15 ω   i ^

v A + 0,555   j ^ = - 0,371 ω   j ^

Resolvendo, encontramos os valores:

ω = - 0,354 k ^   r a d / s

v A = 0,237   m / s

Agora, podemos calcular a velocidade angular da roda através da velocidade de A e do centro instantâneo C:

ω O = v A A C - = 0,237 0,15 2 + 0,1 2 = 1,314 k ^   r a d / s

Finalmente, vamos calcular a velocidade do centro O usando o mesmo conceito acima:

v O = ω O × O C = 1,314 k ^ × 0,15 j ^

v O = - 0,1971   i ^   m / s

Resposta

ω = - 0 , 354 k ^   r a d / s

v O = - 0 , 1971   i ^   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de 4r a d/ s no sentido horário. Determine as velocidades angulares das barras BD e DE.
Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de 4r a d/ s no sentido horário. Determine as velocidades angulares das barras BD e DE.
Na posição mostrada na figura, a barra DE tem uma velocidade angular de 10r a d / s no sentido horário. Sabendo que h = 500m m , determine (a) a velocidade angular da barra FBD, (b) a velocidade do po
Na posição mostrada na figura, a barra DE tem uma velocidade angular de 10 rad /s no sentido horário. Determine (a) a distância h para que a velocidade do ponto F seja vertical, (b) a velocidade corre
Na posição mostrada na figura, a barra AB tem uma aceleração angular nula e uma velocidade angular de 20r a d / s no sentido anti-horário. Determine (a) a velocidade angular da barra BDH, (b) a veloci