Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 66

Na posição mostrada na figura, a barra DE tem uma velocidade angular de 10   r a d / s no sentido horário. Sabendo que h = 500   m m , determine (a) a velocidade angular da barra FBD, (b) a velocidade do ponto F

Passo 1

E aí meus caros! A moda da vez agora é a questão 66!

Bom! Primeiramente, a gente quer determinar as velocidades angulares da barra F D B !

E pra resolver essa questão, mais uma vez vamos recorrer aos versores!

Vamos usar os versores i ^ , j ^ e k ^ , que correspondem respectivamente à...

i ^ → E i x o   x

j ^ → E i x o   y

k ^ → S e n t i d o   d e   r o t a ç ã o   ( - k ^   p a r a   o   h o r á r i o   e   k ^   p a r a   o   a n t i - h o r á r i o )

Feshow!? Agora, vamos posicionar um eixo de coordenadas naquela figura do enunciado. Só pra gente não ficar perdidasso!

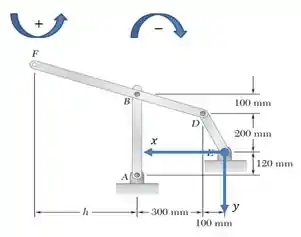
E não podemos esquecer também da tabela de produto vetorial entre versores... Essa é importante!

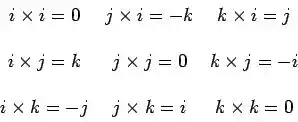
Passo 2

a) Vamos começar nossa análise pela barra D E . A barra está girando a 10   r a d / s no sentido horário. Logo, pela convenção que adotamos...

ω → D E = 10   r a d / s ⤾ = ( 10   r a d / s ) ( - k ^ )

ω → D E = - 10 k ^   r a d / s

Bom! A barra D E está fixa em E . Logo o movimento aí só vai ser de rotação.

Agora se liga na imagem abaixo, que mostra os vetores posição da barra que nos adotamos...

O vetor de posição de D em relação a E , então, é dado por...

r → D / E = - 100 i ^ + 200 j ^   m m

r → D / E = - 0,1 i ^ + 0,2 j ^   m

Logo, a velocidade em D ... Vai ser dada por:

v → D = ω → D E × r → D / E

v → D = ( - 10 k ^   r a d / s ) × [ - 0,1 i ^ + 0,2 j ^   m ]

v → D = 1,0 j ^ + 2,0 i ^     m / s

Passo 3

Em seguida, vamos partir pra barra F B D !

Se liga! A gente tem que F está livre! Então nem faz sentido analisar toda a barra! Basta analisar a parte B D , como mostramos na figura com os vetores posição. A velocidade angular em F vai ser a mesma que em B ! Só com isso, dá pra gente obter o que quer nesse primeiro item!

E nesse caso, vamos ter rotação e translação atuando na barra!

A velocidade angular dela, que ainda não sabemos, é dada por...

ω → B D = ω B D k ^

E a velocidade em B , como já falamos vai ser dada pela soma da translação em D   mais rotação sobre D ...

v → B = v → D + ω → B D × r → B / D

Como o vetor posição de B pra D é dado por...

r → D / B = - 300 i ^ + 100 j ^   m m

r → D / B = - 0,3 i ^ + 0,1 j ^   m

Desse modo...

v → B = v → D + ω → B D × r → D / B

v → B = 1,0 j ^ + 2,0 i ^   + ω B D k ^ × ( - 0,3 i ^ + 0,1 j ^ )

v → B = 1,0 - 0,3 ω B D j ^ + 2,0 - 0,1 ω B D i ^   m / s

Passo 4

Continuando nossa raciocínio, vamos agora barra A B . A velocidade angular dela, que ainda não sabemos, é dada por...

ω → A B = ω A B k ^

Como a velocidade vai ser dada apenas pela rotação, já que A está fixo. Podemos determinar a velocidade em B como...

v → B = ω → A B × r → B / A  

Como o vetor posição de B pra A é dado por...

r → B / A   = 420 j ^   m m

r → B / A   = 0 , 42 j ^   m

Obtemos então, que...

v → B = ω → A B × r → B / A  

v → B = ω A B k ^ × [ 0 , 42 j ^   m ]

v B = - 0,42 ω A B i ^   m / s

Passo 5

Agora, é só uma questão de igualar as velocidades em B que obtivemos nos P a s s o s 3 e 4 ...

v D = - 0,4 ω D E j ^ - 0 , 5 ω D E i ^   m / s = [ - 1,6 - 0,8 ω B D j ^ + 3,2 i ^ ]   m / s

Relacionandos as partes com os mesmos versores. Em j ^ , temos que...

1,0 - 0,3 ω B D = 0

ω B D = 1,0 0,3

ω B D = 3,33   r a d / s  

ω B D = 3,33   r a d / s   ⤿

Em i ^ , por sua vez...

2,0 - 0,1 ω B D = - 0,42 ω A B

2,0 - 0,1 ⋅ 3,33 = - 0,42 ω A B

- 0,42 ω A B = 1,667

ω A B = - 1,667 0,42

ω A B = - 3,969   r a d / s

ω A B ≅ 3,97   r a d / s   ⤾

Pronto! Conseguimos obter a velocidades angulares de F B D , que é dada por...

ω B D = 3,33   r a d / s   ⤿

Passo 6

b) Pra finalizar, vamos obter a velocidade em F !

Bom! A barra B F D está sujeita à rotação e translação! Logo, a velocidade em F , vai ser dada por...

v → F = v → D + ω → B D × r → F / D

v → D e ω → B D a gente já sabe! O problema aí é no r → D / B ! O enunciado nos deu o valor de h , mas ainda tá faltando um dado importante, que é a distância na vertical entre F e D ...

Por isso, vamo fazer um esboço, pra ver se conseguimos descobrir uma forma de achar o que a gente quer.

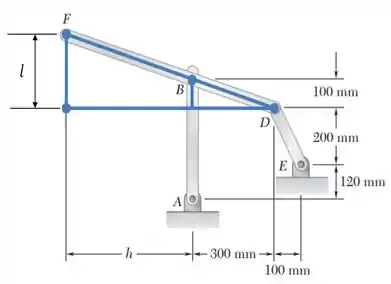
Viu alguma coincidência aí nessa figura! Se não, calma que o produtor vai explicar!

Dá pra obter a distância l que a gente quer simplesmente por semelhança de triângulo. Do seguinte jeitinho abaixo...

l h + 300 = 100 300

Como h = 500   m m :

l = 800 ⋅ 100 300

l = 266,67   m m = 0,2667   m

Desse modo...

r → F / D = 266,67 j ^ - 800,00 i ^   m m

r → F / D = 0,2667 j ^ - 0,80 i ^   m

E então, obtemos que...

v → F = v → D + ω → B D × r → F / D

v → F = 1,0 j ^ + 2,0 i ^   + ( 3,33 k ^ ) × 0,2667 j ^ - 0,80 i ^

v → F = 1,111 i ^ - 1,667 j ^     m / s

Em módulo e com ângulo de orientação...

v F = 1,111 2 + - 1,667 2 ∠ tan - 1 ⁡ - 1,667 1,111

v F = 2,00 ∠ - 56,3 °   m / s

Resposta

a)

ω B D = 3,33   r a d / s   ⤿

b)

v F = 2,00 ∠ - 56,3 °   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade angular do segmento BC e a velocidade do pistão C no instante mostrado.
Determine a velocidade angular dos segmentos BC e CD no instante mostrado.
Se a engrenagem do cubo H e a engrenagem interna R têm velocidades angulares ω H = 5r a d / s e ω R = 20r a d / s , respectivamente, determine a velocidade angular ω s da engrenagem de dentes retos S
Para a roda de Genebra do Prob. 5/56, mostrada aqui novamente, escreva a expressão para a velocidade angular ω 2 da roda ranhurada C durante o acoplamento do pino P e represente graficamente ω 2 para
O braço ranhurado OB oscila em torno da vertical pela ação da manivela rotativa CA com 125 mm de comprimento, onde o pino A se acopla à ranhura. Para uma velocidade constante N = 120r p m da manivela