Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 191

A roda desliza enquanto rola. Se v O = 1,2   m / s e se a velocidade de A em relação a B é de 0,9 2   m / s , localize o centro instantâneo C de velocidade nula e encontra a velocidade do ponto P.

Passo 1

Galera, este é um problema de rolamento com deslizamento. Portanto, o ponto D não é o centro instantâneo de velocidade nula. Porém, o enunciado nos dá informações importantes para a resolução. Vamos lá.

A velocidade relativa de A em relação a B vale:

v A / B = 0,9 2   m / s

Então podemos calcular a velocidade angular da roda, sabendo a distancia AB:

ω = v A B r A B = 0,9 2 0,15 2 = 6   r a d / s

Agora podemos encontrar o Centro Instantâneo C através do centro da roda O. Sabemos que C se localiza em uma posição perpendicular à velocidade do ponto O. Como v O é horizontal:

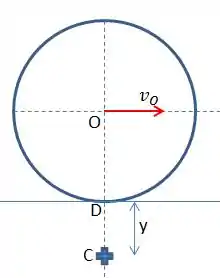
Temos então que:

v O = O C - ω

1,2 = 0,15 + y 6

y = 0,05 m

O C = 0,2 m

Agora vamos para o ponto P. Ele se encontra na horizontal a 75mm de O. Podemos calcular através da velocidade relativa:

v P = v O + ω × r P O

v P = 1,2 i + - 6 k ^ × 0,075 i ^ = 1,2 i - 0,45 j

Como queremos saber o módulo:

v P = 1,2 2 + - 0,45 2 = 1,282   m / s

Resposta

O C = 0,2 m

v P = 1,282   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cilindro de 12 kg sustentado pelos suportes dos mancais em A e B tem um momento de inércia em relação ao eixo vertical z 0 por meio de seu centro de massa G igual a 0,080k g ∙ m 2 . O disco e os sup
Cada uma das duas barras esbeltas uniformes O A e B C possui uma massa de 8k g . As barras estão soldadas em A para formar um elemento com formato de T e estão girando livremente em torno de um eixo h
A haste B de 0,4k g com centro de massa a 55m m de O - O tem um raio de giração de 69m m em relação a O - O . A haste está soldada ao tubo de aço e é livre para girar em torno do eixo horizontal fixo
Um cabo flexível com 60 metros de comprimento, com uma massa de 0,160k g por metro de comprimento, está enrolado em volta do tambor. Com y = 0 , o peso do cilindro de 4k g é necessário para iniciar a
Em 1993 , o ônibus espacial capturou o telescópio Hubble em órbita e fixou-o ao compartimento de carga para reparos, na configuração simulada na figura. Durante o período de reparo era importante limi