Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 8
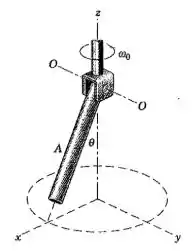
A barra é articulada em torno do eixo O-O do garfo, eu está preso à extremidade do eixo vertical. O eixo gira com uma velocidade angular constante como mostrado. Se está diminuindo na taxa constante , escreva expressões para a velocidade angular e para a aceleração angular da barra.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que essa barra tem o eixo paradinho e tem aquela velocidade angular ali, e nos pede a velocidade e a aceleração para ela. Viu?? Parece que é muita coisa, mas nem é tão difícil assim. Bora lá fazer?? Partiu??
Passo 2
Nosso primeiro passo será analisar o movimento da barra. Como o nosso eixo O-O está paradinho ali e tem essa velocidade angular inicial já estabelecida, podemos tirar pela regra da mão direita (sim, não usamos só em física) para ver que a velocidade angular está no eixo yz.
Agora que sabemos o nosso plano do , vamos calcular quanto vale a velocidade angular. Antes disso, vamos só ver quanto vale cada uma das nossas componentes. No eixo Z, a componente é igual à velocidade angular inicial; no eixo Y, a nossa componente será a variação negativa do ângulo, ou seja, será p.
Passo 3
Pronto!! Com isso, podemos achar qual a nossa aceleração.