Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 28

A roseta de deformação a 45° está montada sobre uma chapa de alumínio. As seguintes leituras foram obtidas para cada extensômero: ∈ a = 475 × 10 - 6 ;   ∈ b = 250 × 10 - 6   e ∈ c = - 360 × 10 - 6 .   Determine as deformações principais no plano.

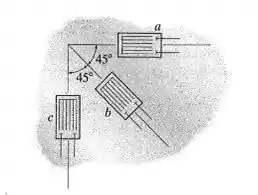
Passo 1

Fala galera, bora pra mais um problema de Resmat? Boraaa!

O problema quer que a gente determine as deformações principais no plano.

Vamos colocar o eixo x positivo na direção de c para baixo. Aí nessa direção a gente tem θ = 0 ° e θ cresce no sentido anti-horário. E assim y positivo aponta para a direita na direção de a .

Então temos que as deformações nos extensômetros e as orientações deles são:

ℇ c = - 360 × 10 - 6 → θ = 0 ° ℇ b = 250 × 10 - 6 → θ = 45 ° ℇ a = 475 × 10 - 6 → θ = 90 °

A ideia é achar as deformações normais e de cisalhamento no plano x y . E através delas achar as deformações principais. Vamos lá!

Passo 2

Com esse sistema de referências que a gente escolheu, podemos achar as deformações nos nossos eixos. No eixo x vamos ter:

ℇ x = ℇ c ∴ ℇ x = - 360 × 10 - 6

Para o eixo y :

ℇ y = ℇ a ∴ ℇ y = 475 × 10 - 6

E por essa fórmulinha aqui a gente acha a deformação de cisalhamento no plano:

γ x y = 2 ε b - ε a + ε c

Substituindo os nossos dados e calculando:

γ x y = 385 × 10 - 6

Aí com isso a gente consegue achar as principais. Vem!

Passo 3

Para calcularmos as deformações principais vamos usar a seguinte fórmula:

ℇ 1,2 = ℇ x + ℇ y 2 ± ℇ x - ℇ y 2 2 + γ x y 2 2

Subsituindo, ficamos com:

ℇ 1 = ℇ x + ℇ y 2 + ℇ x - ℇ y 2 2 + γ x y 2 2

ℇ 1 = - 360 × 10 - 6 + 475 × 10 - 6 2 + - 360 × 10 - 6 - 475 × 10 - 6 2 2 + 385 × 10 - 6 2 2

ℇ 1 ≈ 517 × 10 - 6

E para ℇ 2

ℇ 2 = ℇ x + ℇ y 2 - ℇ x - ℇ y 2 2 + γ x y 2 2

ℇ 1 = - 360 × 10 - 6 + 475 × 10 - 6 2 - - 360 × 10 - 6 - 475 × 10 - 6 2 2 + 385 × 10 - 6 2 2

ℇ 2 ≈ - 402 × 10 - 6

Resposta

ℇ 1 = 517 × 10 - 6 ℇ 2 = - 402 × 10 - 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O estado plano de tensão mostrado ocorrerá em um ponto crítico em uma peça fundida de alumínio que é feita de uma liga para a qual σ L T = 69M P a e σ L C = 172,4M P a . Usando o critério de Mohr, det
A barra de alumínio fundido indicada na figura é feita de uma liga para a qual σ L T = 70M P a e σ L C = 175M P a . Sabendo que a intensidade T dos torques aplicados está crescendo lentamente e usando
O estado plano de tensão mostrado ocorrerá em um ponto crítico em um tubo feito de uma liga de alumínio para a qual σ L T = 75M P a e σ L C = 150M P a . Usando o critério de Mohr, determine a tensão d
A barra de alumínio fundido indicada na figura é feita de uma liga para a qual σ L T = 60M P a e σ L C = 120M P a . Usando o critério de Mohr, determine a intensidade do torque T para a qual se espera
Um componente de máquina é feito de um tipo de ferro fundido para o qual σ L T = 55,2M P a e σ L C = 137,9M P a . Para cada um dos estados de tensão indicados, e usando o critério de Mohr, determine a