Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 39
A rotação da alavanca é controlada pelo movimento do disco em contato cujo centro recebe uma velocidade horizontal . Determine a expressão para a velocidade angular da alavanca em termos de .
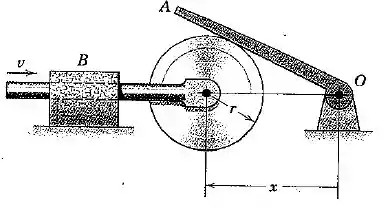
Passo 1
Para encontrar a velocidade angular da alavanca precisamos definir o seu ângulo de deslocamento:
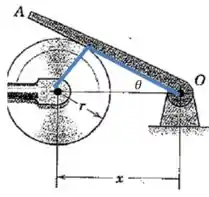
E agora podemos derivar essa equação em relação ao tempo, lembrando que é uma constante:
E é a velocidade angular que queremos encontrar, e é o negativo da velocidade com que o disco é empurrado para frente.
Passo 2
Reorganizando nossa equação:
E podemos escrever essa tangente se olharmos para o desenho:
Resposta
A velocidade angular da alavanca é .
Exercícios de Livros Relacionados
No Problema 15.192, determine (a) a velocidade do ponto A, (b) a aceleração do ponto A.
O braço BCD em forma de L gira em torno do eixo z com uma velocidade angular constante ω 1 de 5r a d/ s . Sabendo que o disco de 150m m de raio gira em torno de BC com uma velocidade angular constante
Um disco de 100 mm de raio gira à taxa constante ω 2 = 4r a d/ s em torno de um eixo apoiado em uma estrutura presa a uma barra horizontal que gira à taxa constante ω 1 = 5r a d / s . Para a posição m
Um disco de 100m m de raio gira à taxa constante ω 2 =4r a d/ s em torno de um eixo apoiado em uma estrutura presa a uma barra horizontal que gira a uma taxa constante ω 1 = 5r a d/ s . Sabendo que θ
Um cano de canhão de comprimento O P =4m está montado sobre uma torre blindada do modo mostrado na figura. Para manter o cano com a mira em um alvo móvel, o ângulo azimutal β é aumentado a uma taxa d