Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 35
O carretel de cabo telefônico rola sem deslizar sobre a superfície horizontal. Se o ponto no cabo possui uma velocidade para a direita, calcule a velocidade do centro e a velocidade angular do carretel. (Tenha cuidado para não cometer o erro de supor que o carretel rola para a esquerda.)
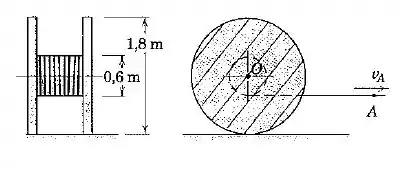
Passo 1
Vamos chamar de a velocidade do centro do carretel. Nesse caso, temos:
E o raio já foi dado na figura do enunciado:
Para aproveitar o valor de que foi dado no enunciado, precisamos usar a semelhança de triângulos:
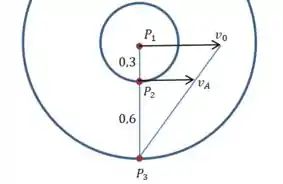
E então por semelhaça de triângulos podemos construir a seguinte relação:
Passo 2
E substituindo com a primeira relação que escrevemos:
E agora podemos calcular a velocidade do centro:
Resposta
A velocidade do centro é e a velocidade angular é .
Exercícios de Livros Relacionados
A haste uniforme AB de peso W é liberada do repouso quando β = 70 °. Assumindo que a força de atrito entre a extremidade A e a superfície é grande o suficiente para evitar o deslizamento, determine im
A haste uniforme AB de peso W é liberada do repouso quando β = 70 ∘ . Assumindo que a força de atrito é zero entre a extremidade A e a superfície, determine imediatamente após a liberação (a) a aceler
Uma placa uniforme de massa m é suspensa em cada uma das formas mostradas. Para cada caso, determine imediatamente após a conexão em B ter sido liberada (a) a aceleração angular da placa, (b) a aceler
A barra estreita AB de peso W é mantida em equilíbrio por dois contrapesos cada um pesando 1 2 W . Se o fio em B for cortado, determine a aceleração naquele instante (a) do Ponto A, (b) do Ponto B.
O centro de massa G de uma roda de 5 kg de raio R = 300 mm está localizado a uma distância r = 100 mm de seu centro geométrico C. O raio de rotação centróide é k = 150 mm. Conforme a roda gira sem des