Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 40

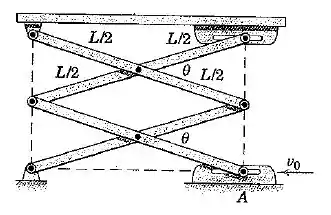
O movimento vertical da plataforma de trabalho é controlado pelo movimento horizontal do pino A . Se A possui uma velocidade v 0 para a esquerda, determine a velocidade vertical v da plataforma para qualquer valor de θ .

Passo 1

Aqui é importante pensar em termos geométricos, vamos tentar escrever a altura y da plataforma em termos das grandezas que foram dadas no enunciado.

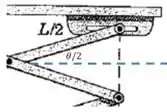
Qual é o comprimento da linha pontilhada preta vertical?

h = 2 L 2 sen ⁡ θ 2 = L sen ⁡ θ 2

E a altura total da plataforma é:

y = 2 h = 2 L sen ⁡ θ 2

Passo 2

Agora podemos derivar essa equação em relação ao tempo:

y = 2 L sen ⁡ θ 2

y ˙ = L   θ ˙ cos ⁡ θ 2

Precisamos achar alguma forma de substituir θ ˙ .

Passo 3

Vamos chamar de x a posição do suporte que se move para a esquerda com velocidade v 0 . Podemos nos basear no mesmo desenho de antes para encontrar uma equação para x :

x = L cos ⁡ θ 2

E agora derivando em relação ao tempo:

x ˙ = - v 0 = - L θ ˙ 2   sen ⁡ θ 2

v 0 = L θ ˙ 2 sen ⁡ θ 2

E agora podemos isolar a velocidade angular θ ˙ :

θ ˙ = 2 v 0 L csc ⁡ θ 2

E substituindo isso na equação anterior:

y ˙ = L   θ ˙ cos ⁡ θ 2

y ˙ = L   2 v 0 L csc ⁡ θ 2   cos ⁡ θ 2

y ˙ = v = 2 v 0 cot ⁡ θ 2

Resposta

A velocidade vertical da plataforma é v = 2 v 0 cot ⁡ θ 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A empilhadeira mostrada na figura tem a massa de 1,125 k g e é usada para elevar um caixote de massa m = 1,250 k g . Sabendo que a empilhadeira está em repouso, determine (a) a aceleração para cima pa
Uma placa retangular uniforme tem massa de 5 k g e é mantida na posição por três cordas mostrado na figura. Determine o maior valor de θ para que ambas nas cordas AD e BE permaneçam esticadas imediata
Resolva o Problema 16.11, considerando que a aceleração a do suporte é dirigida para baixo.
Considerando que a massa de um barril cheio somado com seu conteúdo tem uma massa combinada de 100 k g . Um cilindro C é ligado ao barril na altura h = 550 m m como mostra figura. Sabendo que μ s = 0,
O suporte mostrado na figura é usado para transportar uma lata cilíndrica de um nível de elevação para outro. Sabendo que μ s = 0,25 entre a lata e o suporte, determine (a) a intensidade da aceleração