Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 6
Sabendo que o momento mostrado atua em um plano vertical, determine a tensão no:
- Ponto A
- Ponto B
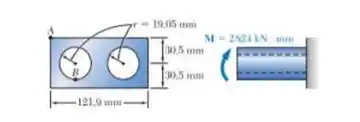
Passo 1
Fala galerinha, estamos aqui iniciando o nosso capitulo 4, e o enunciado de cara já vem pedindo para determinarmos a tensão normal nos pontos A e B sem pedir licença, mas pode ficar de boas, ele quer tensão, então vamos dar tensão a ele.
Pra isso temos que lembrar que a nossa fórmula de tensão quando temos um momento agindo é dada por:
E cada terminho desse é bem tranquilo de determinar, beleza? Então vamos lá.
Passo 2
Existem dois termos que não dependem em nada dos pontos A e B, então vamos determinar eles primeiro, já que são comuns aos dois:
- M (momento fletor)
- I (momento de inércia)
Esse é bem fácil, mas temos que tomar muito cuidado com o sinal, do jeito que ele está na nossa figura, podemos ver que ele gira no sentido horário, quando ele girar no sentido horário, vai ser como se ele fosse um momento apontando para a esquerda da nossa figura, assim, o seu desenho vai ser dado por:
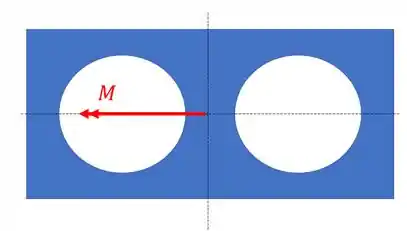
Porque isso é importante? Porque sempre que o nosso momento estiver apontando para a esquerda ele será POSITIVO na nossa fórmula, beleza? Então podemos definir que:
Esse vai ser tranquilo também, no caso, temos uma seção retangular furada, sabemos que a fórmula do momento de inércia para retângulos é dada por:
Porém como a nossa seção é furada, precisamos fazer a área da seção total subtraída da área faltante no centro, que são círculos, e o momento de inércia de círculos é dado por:
Para termos o momento de inércia da seção vazada, teremos que:
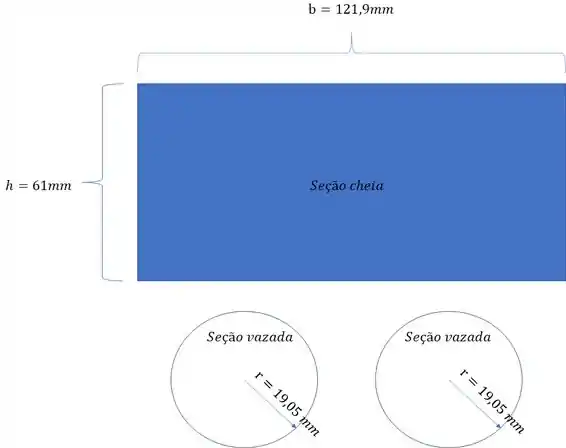
Assim teremos que:
Agora só precisamos do y que muda de acordo com o ponto que queremos saber a tensão.
Passo 3
Nesse caso é bem simples determinar o y, porque pensa só, como a seção é simétrica, a linha neutra passa bem no centro da seção, assim, basta pegarmos a distancia de cada ponto até a LN, e assim vamos ter a tensão naquele ponto, dessa forma temos que:
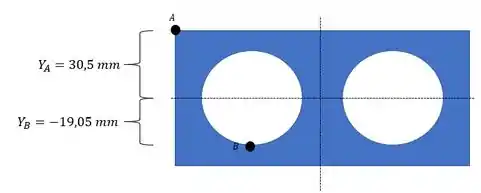
Muito importante ver que se estamos acima da LN o valor de y é positivo, e se estamos abaixo, ele é negativo, assim, podemos ver que as tensões em cada ponto serão dadas por: