Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 67a
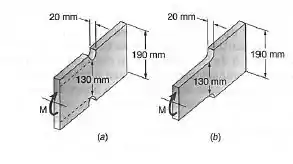
Um momento é aplicado na extremidade de uma barra de aço. Determinar a máxima tensão na barra se: (a) a barra é projetada com entalhes semi-circulares de , como mostrado na Fig. a;
Passo 1
Temos um elemento flexionado, com um entalhe. Nesse caso, as tensões máximas ocorrem onde há concentração de tensões, ou seja, onde há mudança de seção. E para descobrir essas tensões a gente usa a fórmulinha:
Nossos dados são:
- Altura maior da seção flexionada:
- Altura menor (na menor seção do entalhe):
- Espessura:
- Raio do entalho:
- Momento aplicado:
Vem comigo!
Passo 2
A seção onde ocorre a maior tensão é a menor seção, de altura . Ela é um retângulo, então o momento de inércia fica:
E a tensão máxima vai ocorrer na maior distância do eixo neutro nessa seção:
Passo 3
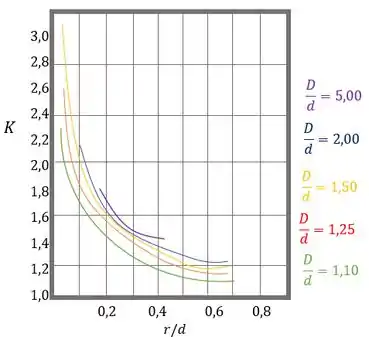
Agora a gente precisa achar . Vamos usar o gráfico:
Para a gente:
Aí é só ir na curva onde (a amarelinha) e achar o valor de para :
Passo 4
Calma, falta pouco. Só substituir todos os nossos dados na fórmulinha:
Ufa! Conseguimos!