Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 74
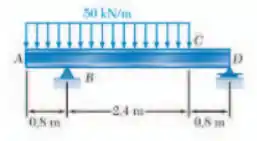
Sabendo que a tensão normal admissível para o aço utilizado é , escolha a viga com seção em perfil de mesa larga mais econômica que suporta o carregamento dado.
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.
Como queremos selecionar o perfil mais econômico que suporta o carregamento dado, devemos, primeiramente, esboçar o DCL:
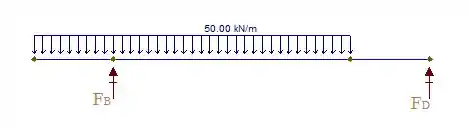
Em seguida, vamos calcular as reações de apoio. Para isso, vamos utilizar as equações de equilíbrio:
E também:
Com isso, podemos calcular as equações para a força cortante. Para isso vamos dividir nossas vigas em segmentos e assim, utilizar as equações de equilíbrio. Para o primeiro segmento, dado por , temos:
Já para o segmento , temos:
E para o segmento , temos:
Portanto, podemos esboçar o diagrama de força cortante a partir dessas equações. Fica assim:
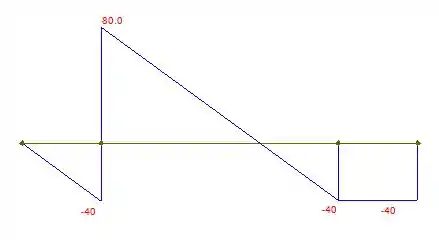
Com o esboço do diagrama, vamos marcar como , o ponto do diagrama em que . Substituindo na equação para , temos:
Passo 2
Em seguida, vamos calcular as equações para o momento fletor. Para isso, devemos integrar em as equações de força cortante em cada segmento. Fica assim:
Para o segmento , temos:
Para o segmento temos:
E para o segmento , temos:
E também, o diagrama de momento:
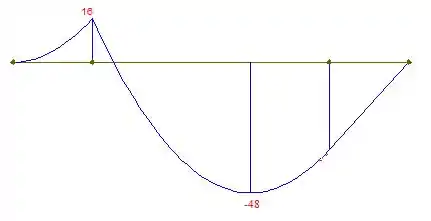
Com os diagramas traçados, podemos ver que o momento fletor máximo absoluto ocorre no ponto onde a força cortante é . Lembra daquele ponto que a gente encontrou? Vamos utilizar ele para encontrarmos o ponto de máximo, esse conceito vem lá do cálculo 1. Logo, substituindo:
Agora que temos o momento fletor absoluto, bora encontrar o perfil mais econômico.
Passo 3
Já temos o momento máximoe o enunciado nos forneceu a tensão normal admissível . Então, basta encontrarmos a outra variável da qual a tensão normal depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é o valor mínimo admissível do módulo de resistência da seção da viga. Subsituindo:
E então, para determinarmos o perfil mais econômico devemos olhar no ábaco o valor mínimo admissível do módulo de resistência imediamente maior que o que encontramos. Assim, o perfil escolhido é:
Que possui .
É isso, galera! Bora fazer mais exercícios pra ficar craque.