Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 46

Quatro cantoneiras de aço 1,202 x 102 x 9,5 e uma placa de 12 x 400 mm são parafusadas de modo a formar a viga de seção transversal mostrada. Os parafusos tem diâmetro de 22mm e são espaçados longitudinalmente a cada 120mm. Sabendo que a viga está submetida a uma força cortante vertical de 240 kN, determine a tensão de cisalhamento média em cada parafuso.

Passo 1

Fala gurizada, tudo certo? O enunciado diz que a viga está submetida a uma força cortante vertical de 240 kN. Então bora indicar a tensão de cisalhamento média em cada parafuso. Considere o esboço abaixo ;)

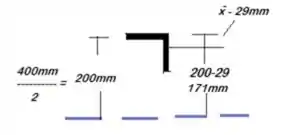
Considere os dados:       A = 1845 mm²,     I = 1,815 x 10 6 mm²

Q = 1845   m m 2 171   m m =     315,5   x   10 ³   m m   ³ =   315,5   x   10 - 6   m 4

Passo 2

Para placa de 12 mm 400 mm e quatro ângulos

I = 1 12 ( 12 m m ) ( 400 m m ) ³ + 4 1,815   x   10 6 m m 4 + ( 1845 m m ² ) ( 171 m m ) ²

= 287,06   x   10 6 m m 4 = 263,78   x   10 - 6 m 4

Passo 3

Um ângulo:

q = V Q I = ( 240 k N ) ( 315,5   x   10 - 6 m ³ ) 287,06   x   10 - 6 m 4 = 263,78   k N / m

Calculando a força temos:

F = q s = ( 263,78   k N / m ) ( 0,120   m )   31,65   k N

Considerando o diâmetro = 22 m m     temos:

t = F A = 31,65 k N π 4 ( 0,022 m ) ² = 83,3   M P a

Resposta

83,3   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o P r o b . 5.36 , considerando que a viga seja submetida a uma força cortante horizontal V .
Quatro perfis de aço cantoneira 102 x 102 x 9,5 e uma placa de aço de 12 x 40 0m m são aparafusadas juntas para formar uma viga como a seção transversal mostrada. Os parafusos são de 22 m m de diâmetr
Resolver o Prob.5.40, considerando que a altura da placa é aumentada de 400m m para 600 m m .
Três pranchas são conectadas como mostrada, por parafusos de 16 m m de diâmetro e espaçados de 300m m , ao longo do eixo longitudinal da viga. Para uma força cortante vertical de 13350N , determinar a
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.