Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 61
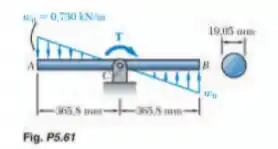
Sabendo que a viga está em equilíbrio sob o carregamento mostrado, trace os diagramas de força cortante e momento fletor para essa viga e determine a tensão normal máxima provocada pelo momento fletor.
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora acabar com esse livro de resmat.
Neste problema, podemos ver que a estrutura está em equilíbrio pelas próprias cargas e não há reação de apoio.
Logo, basta utilizar os esforços para calcular os diagramas. Neste caso, temos cargas distribuídas e nosso diagrama de cortante terá a seguinte cara:
Já o diagrama de momento, será:
Passo 2
Agora, com os diagramas, basta calcular a tensão máxima, substituindo o momento máximo na fórmula da tensão. A tensão é dada por:
Onde é o momento fletor, é a distância da linha neutra, que neste caso vale metade do diâmetro, e é o momento de inércia. Logo:
Portanto:
E pronto, achamos a tensão máxima pedida.