Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 56

Cinco tiras de metal, cada uma com 0,5 x 1,5   i n de seção transversal, são unidas para formar uma viga composta, mostrada na figura. O modulo de elasticidade é de 30 × 10 6 p s i para o aço, de 15 × 10 6   p s i para o latão e 10 × 10 6   p s i para o alumínio. Sabendo que a viga é flexionada em torno do eixo horizontal por um momento de 12   k i p ∙ i n , determine:

  1. A tensão máxima em cada um dos três metais
  2. O raio de curvatura da viga composta.

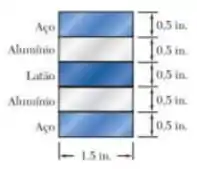
Passo 1

Quando temos mais de um material na nossa barra precisamos converter todos ela para um deles para facilitar o nosso cálculo.

Sabemos que o nosso fator a ser calculado é dado por:

n = E p a r t e   t r a n s f o r m a d a   E p a r t e   i n t a c t a  

Vamos então fazer o seguinte, vamos manter como intacto o Aço, e vamos transformar em aço o latão e o alumínio, sendo assim vamos ter dois fatores de transformação, sendo assim teremos que:

n l a t ã o = E l a t ã o   E a ç o   = 15 × 10 6 30 × 10 6 = 0,5

n a l u m í n i o = E a l u m í n i o   E a ç o   = 10 × 10 6 30 × 10 6 = 0,33

E como temos duas mudanças, precisamos modificar a largura das chapas de latão e de alumínio, e como elas foram as transformadas, então o aço vai se manter, e o latão e alumínio vão ser modificados:

b ' = n b

b ' l a t ã o - a ç o = n l a t ã o b l a t ã o = 0 , 50   .   1,5 = 0,75   i n

b ' a l u m í n i o - a ç o = n a l u m i n i o b a l u m i n i o = 0,33   .   1,5 = 0,50   i n

Sendo assim a nova seção é dada por:

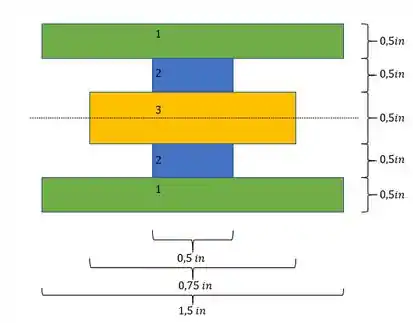
Nosso objetivo é determinar as tensões, e a fórmula que calcula a tensão na estrutura intacta, é dada por:

σ x = - M y I

E a fórmula para calcular as tensões nas barras que foram transformadas é dada por:

σ x = - n M y I

Ou seja, temos que tomar cuidado de usarmos o coeficiente de transformação correto, na barra correta.

Agora já podemos determinar o momento de inércia e o y da nossa fórmula.

Passo 2

Como a seção é simétrica, já sabemos onde está a LN, então basta calcularmos o momento de inércia, que para a nossa seção será dado por:

I = 2 ( I 1 + A 1 d 1 2 ) + 2 ( I 2 + A 2 d 2 2 ) + ( I 3 + A 3 d 3 2 )

Em que I   e   A são as inércias e áreas, respectivamente, de cada seção transformada, e d é a distância do centroide de cada seção até a LN, que podemos ver aqui embaixo.

I = 2 ( 1,5 × 0,5 3 12 + 1 , 5 × 0,5 × 1 2 ) + 2 ( 0 , 50 × 0,5 3 12 + 0 , 5 × 0,5 × 0,5 2 ) + ( 0,75 × 0,5 3 12 )

I = 1,674   i n 4

Agora só precisamos determinar os valores de y para cada uma das barras, sendo assim teremos que ver o próximo passo.

Passo 3

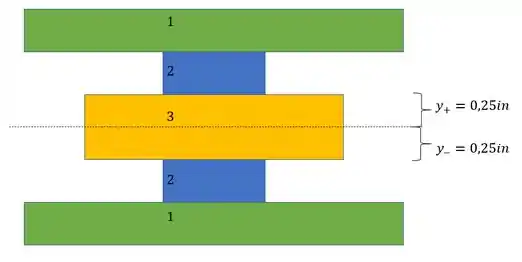
Pelo enunciado, o nosso objetivo é determinar a máxima tensão em cada seção, logo, precisamos determinar y para cada seção, e lembrando que temos parcelas intactas e parcelas transformadas, ou seja, algumas não possuem fator de transformação multiplicando a tensão e outros tem, sendo assim teremos que:

  • y - positivo e negativo (latão)

  • y - positivo e negativo (aluminio)

  • y - positivo e negativo (aço)

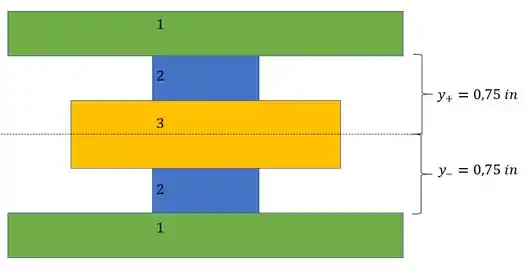
    • Passo 4

    Calculando a tensão no aço primeiro, teremos que:

    M = 12   k i p ∙ i n

    y - - = - 1 , 25   i n

    I = 1,674   i n 4

    σ a ç o = - M y I

    Substituindo, teremos que:

    σ max ⁡ - a ç o = - 12   k i p ∙ i n - 1 , 25 i n 1,674   i n 4 = 8,96   k i p i n 2 = 8,96   k s i

    Calculando a tensão no latão, teremos que:

    M = 12   k i p ∙ i n

    y - - = - 0 , 2 5   i n

    I = 1,674   i n 4

    σ l a t ã o = - n M y I

    Substituindo, teremos que:

    σ max ⁡ - l a t ã o = - 0,5 12   k i p ∙ i n - 0 , 2 5 i n 1,674   i n 4 = 0,896 k i p i n 2 = 0,896   k s i

    Calculando a tensão no alumínio, teremos que:

    M = 12   k i p ∙ i n

    y - - = - 0,75   i n

    I = 1,674   i n 4

    σ a l u m i n i o = - n M y I

    Substituindo, teremos que:

    σ max ⁡ - a l u m i n i o = - 1 3 × 12   k i p ∙ i n - 0,75 i n 1,674   i n 4 = 1,792   k i p i n 2 = 1,792   k s i

    Passo 5

    Agora o nosso objetivo é determinar o raio de giração, e sabemos que o cálculo é feito da seguinte maneira:

    1 ρ = M I E

    ρ = E I M

    Como tudo foi convertido para aço, podemos usar o modulo de elasticidade do aço, sendo assim teremos que:

    ρ = 30 × 10 6 p s i × 1,674   [ i n 4 ] 12   [ k i p ∙ i n ]

    Sabemos que:

    1 p s i = 0,001   k s i

    Assim teremos que:

    ρ = 30 × 10 6 0,001 k s i × 1,674   [ i n 4 ] 12   [ k i p ∙ i n ]

    ρ = 30 × 10 3 k i p i n 2 × 1,674   [ i n 4 ] 12   [ k i p ∙ i n ]

    ρ = 4185   i n = 349   f t

    Resposta

  • A)

    • σ max ⁡ - a ç o = 8,96   k s i

    σ max ⁡ - l a t ã o = 0,896   k s i

    σ max ⁡ - a l u m i n i o = 1,792   k s i

  • B)

ρ = 4185   i n = 349   f t

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga composta é feita de aço A-36 (A) e latão vermelho C83400 (B) e tem a seção transversal mostrada na figura. Se for submetida a um momento M = 6,5 kN.m, determine a tensão máxima no latão e no aç
Uma tira bimetálica é feita de pedaços de alumínio 2014-T6 e latão vermelho C83400 e tem a seção transversal mostrada na figura. Um aumento na temperatura provoca a curvatura de sua superfície neutra
A viga composta é feita de alumínio 6061-T6 (A) e latão vermelho C83400 (B). Se a altura h = 40 mm, determine o momento máximo que pode ser aplicado à viga se a tensão de flexão admissível para o alum
A viga composta é feita de alumínio 6061-T6 (A) e latão vermelho C83400 (B). Determine a dimensão h da tira de latão de modo que o eixo neutro da viga esteja localizado na costura dos dois metais. Qua
A viga em U de aço é usada para reforçar a viga de madeira. Determine a tensão máxima no aço e na madeira se a viga for submetida a um momento M = 1,2 kN.m. Eaço = 200 GPa, Emad = 12 GPa.