Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 101
Usando funções de singularidade, escreva as equações definindo a força cortante e o momento fletor para a viga e o carregamento mostrados. Use a equação obtida para para determinar o momento fletor no ponto e verifique a sua resposta desenhando o diagrama de corpo livre da parte da viga à direita de .
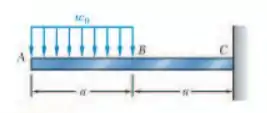
Passo 1
Fala aí, galera. Tudo certo? Bora fazer mais questões.
Primeiro, precisamos identificar em qual caso o carregamento se enquadra. Podemos ver que o carregamento é dado pela seguinte função:
O próximo passo é integrar a função para o carregamento a fim de obtermos a equação para força cortante. Fica assim:
Essa é a equação para a força cortante. Bora para a equação do momento fletor. Para a encontrarmos precisamos integrar a equação de força cortante, temos:
Agora que encontramos a equação para o momento fletor, podemos encontrar o momento fletor no ponto pedido, que é o ponto . Ele está na posição da viga, assim, vamos substituir na nossa equação:
Passo 2
Em seguida, o problema nos pede para verificar se esta resposta é válida. Para isso, vamos esboçar o DCL e então, a partir das equações de equilíbrio, vamos determinar o momento em .
Bora esboçar o DCL, ele vai ficar assim:
Com isso, pelas equações de equilíbrio, temos:
Opa, com isso a gente pode ver que os momentos são iguais. Bora zerar esse livro.