Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 166

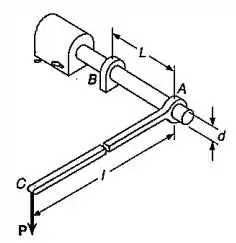
Sabendo-se que τ a d m = 50   M P a , determinar o menor diâmetro permissível para o eixo maciço A B , quando P = 670   N , l = 460   m m e L = 75   m m . Incluir o efeito das tensões de cisalhamento, causadas pela carga transversal.

Passo 1

Fala aí galera, bora pra mais uma questão de Resmat. O primeiro passo é determinar os momentos de inércia das partes da estrutura:

I A B = I H J = 30 × 6 3 12 = 540 m m 4

I D E = I F G = 30 × 4 3 12 = 160 m m 4

I A H = 6 × 90 3 12 = 364500 m m 4

Logo, o momento de inércia total será:

I = ∑ I = 365900 m m 4

Passo 2

Agora, vamos pegar parte por parte para fazermos nossa análise. Para a parte AB, temos que:

Q = 3 × 6 × 30 = 540 m m ³

Logo:

τ = V Q I t = 35000 × 540 6 × 540 = 5833,33 M P a

Logo:

F 1 = τ A = 6 × 30 × 5833,33 = 1050000 N

Passo 3

Agora, faremos o mesmo para AH:

Q = 45 × 6 × 22,5 = 6075 m m ³

Logo:

τ = V Q I t = 35000 × 6075 6 × 160 = 221484,37 M P a

Logo:

F 2 = τ A = 90 × 6 × 221484,375 = 119601562,5 N

Passo 4

Portanto, o centro de cisalhamento será dado por:

∑ M = V e

Logo:

35000 e = 30 × 1050000 + 3 × 119601562,5

e = 11151,56 m m

Resposta

e = 11151,56 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Várias forças são aplicadas à montagem tubular indicada. Sabendo-se que os diâmetros, interno e externo, do tubo são iguais a 38 m me45 m m , respectivamente, determinar:Os planos e as tensões princip
Uma força vertical de 18k N é aplicada na extremidade A da barra AB, que é soldado a um tubo de alumínio extrudado de espessura uniforme de 6mm. Determinar as tensões principais e a máxima tensão de c
Resolver os P r o b s . 6 . 8 e 6.1 2 , usando o círculo de mohr.
Resolver os P r o b s . 6 . 7 e 6.1 1 , usando o círculo de mohr.
Resolver os P r o b s . 6.6 e 6.10 , usando o círculo de mohr.