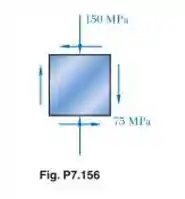
Sabe-se que existe um estado plano de deformação na superfície de um componente de máquina. Sabendo que E = 200 GPa e G = 77,2 GPa, determine a direção e a intensidade das três deformações específicas principais (a) por meio da determinação do estado de deformação correspondente [use a Equação (2.43) e a Equação (2.38)] e em seguida utilize o círculo de Mohr para deformação; e (b) utilize o círculo de Mohr para determinar os planos e as tensões principais e então determine as deformações correspondentes.

Tá legal! Vamos começar escrevendo as tensões dadas pelo elemento diferencial:

Beleza! E nós sabemos que as deformações nas direções x, y e a deformação de cisalhamento podem ser dadas por:

Beleza, então precisamos calcular o valor de para utilizar as equações acima. Sabemos que o módulo de cisalhamento pode ser escrito como:

Substituindo os valores conhecidos, temos:

Então, as deformações nas direções x, y e a deformação de cisalhamento serão:

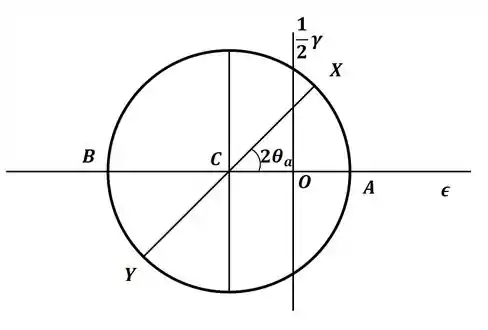
Com esses pontos podemos desenhar o círculo de Mohr, que será dado por:

Agora, com o círculo de Mohr, vamos encontrar a expressão da deformação média, que será dada por:

E, o nosso raio do círculo será dado por:

Agora vamos encontrar a direção principal para o ponto A, que será dada por:

E, como sabemos que a outra direção principal B fica do outro lado do círculo, ou seja, a 180°, como cada grau de rotação do elemento diferencial representa dois graus de rotação no círculo, para obter a direção principal em B, basta somar 90° ao valor obtido para , então teremos:

Agora, as deformações principais em A e B serão dadas por:

E a deformação principal C, que é dada por:

Ufa! Fechamos a letra (a), agora bora pra (b).

Agora para a letra (b), vamos desenhar o círculo de Mohr de tensões com o elemento diferencial dado lá no enunciado, então teremos:

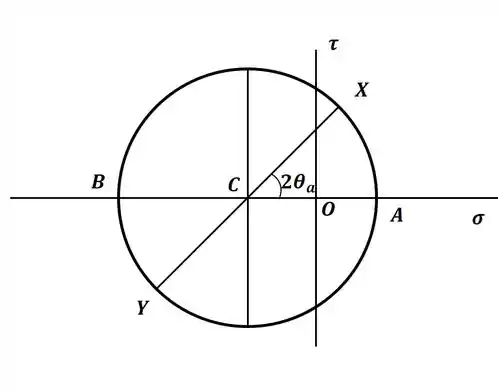
Então, nesse caso, teremos que as tensões principais em A e B serão dadas por:

Então vamos precisar calcular a tensão média e o raio do círculo de Mohr das tensões. Começando pela tensão média, teremos:

E, o raio do círculo será dado por:

Então, as tensões principais serão:

Agora, vamos encontrar os planos principais, para a direção principal em A, teremos:

E, como sabemos que a outra direção principal B fica do outro lado do círculo, ou seja, a 180°, como cada grau de rotação do elemento diferencial representa dois graus de rotação no círculo, para obter a direção principal em B, basta somar 90° ao valor obtido para , então teremos:

Agora conseguimos calcular as deformações correspondentes, que serão dadas por:

Shooow! Fechamos a letra (b) e o exercício como um todo, valeeu!