Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 8
Para o suporte tipo gancho do Problema 2.1, usando trigonometria e sabendo que a intensidade de é , determine (a) a intensidade requerida da força se a resultante das duas forças aplicadas em for vertical, (b) a intensidade correspondente de .
Passo 1
Bom galera, vamos começar extendentos as forças de forma paralelas pra formar um paralelogramo e traçamos a força resultante na interseção, bem assim:
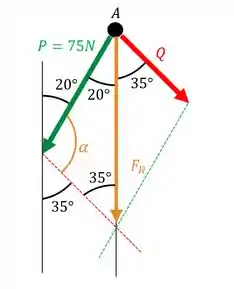
Agora a gente pode usar a lei dos cossenos com isso, mas pra isso precisamos do ângulo , que é:
Passo 2
Show de bola, agora podemos usar a lei dos senos para encontrar a força :
Vamos fazer aquele bom e velho “meio pelos extremos”:
Passo 3
Por fim, usamos a lei dos cossenos para encontrar a resultante, fazemos bem assim:
Resposta
Exercícios de Livros Relacionados
Determine o valor da soma vetorial V = V 1 + V 2 e do ângulo θ x que V faz com o eixo positivo x . Complete tanto a solução gráfica quanto a algébrica.
Suponha que dois valores adimensionais valem exatamente A = 6,67 e B = 1,726 . Usando as regras para algarismos significativos, apresentadas neste capítulo, calcule os valores de ( A + B ) , ( A - B )
Uma força é especificada pelo vetor F = 120 i - 160 j + 80kN . Calcule os ângulos entre F e os eixos positivos x , y e z .