Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 1.Problemas - Ex. 2
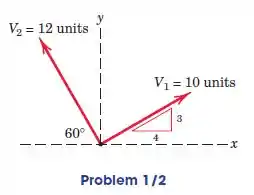
Determine o valor da soma vetorial e do ângulo que faz com o eixo positivo . Complete tanto a solução gráfica quanto a algébrica.
Passo 1
Esse é um problema simples, rapidão você vai entender!
O enunciado pede soma vetorial e do ângulo que faz com o eixo positivo . Vamos começar construindo o gráfico. Veja que, traçando um paralelogramo, a diagonal dele será o nosso vetor .
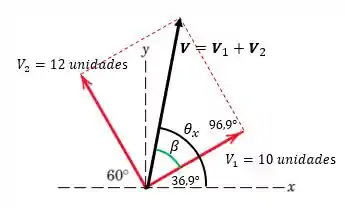
Observe que não temos o ângulo que faz com o eixo , mas temos um triângulo no qual podemos fazer uma relação. Chamaremos ele de :
Esse valor já foi representado no gráfico.
Como ele pede a solução gráfica, faça o gráfico para verificar os resultados.
Passo 2
Fazendo algebricamente, usamos a lei dos cossenos:
Passo 3
Vamos calcular, por meio da lei dos senos, o valor de para, posteriormente, encontrarmos o valor de .
E, por fim,