Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 95
Se a tensão de apoio admissível para o material sob os apoios em e for , determine a carga máxima que pode ser aplicada à viga. As seções transversais quadradas das chapas de apoio são e , respectivamente
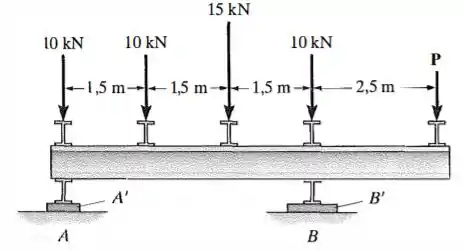
Passo 1
Oláaaa, querido! Cê tá bem?
Queremos encontrar o maior valor de para as condições do problema.
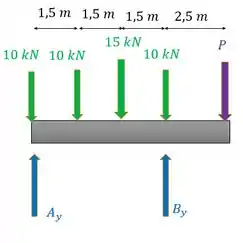
Ele nos forneceu as dimensões das chapas de apoio e , e a tensão admissível em cada uma delas.
O que a gente precisa fazer é achar que pode deixar na tensão admissível limite e depois achar que pode deixar no seu limite. E aí o máximo para a estrutura é o menor entre essas duas situações.
Por que? Porque o menor vai ser o que deixa um dos apoios no limite e o outro apoio fica deboas.
Se a gente usar o maior , significa que um apoio vai estar no limite mas o outro já vai ter ruído porque o limite dele já tinha sido atingido no menor. Então essa situação não é possível porque precisamos dos dois apoios da viga funcionando para ela fica de pé hehe
Passo 2
Vamos começar achando o valor de para o limite do apoio . Vamos achar uma equação que tenha só e como incógnitas, calculando o somatório de momentos em .
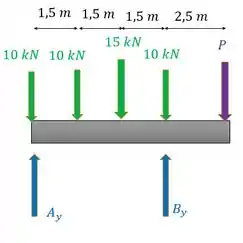
Adotando o sentido anti-horário como positivo teremos
Passo 3
Aí pensa: queremos que o apoio esteja no limite. Então a força que ele suporta é a força limite que suporta. Para achar ela a gente pode usar a expressão da tensão normal admissível:
A força em é e a área do suporte é . E a tensão admissível é . Substituindo essas coisas e isolando :
Dica: a resposta inicial deu em newtons porque usamos e .
Podemos substituir na nossa equação do passo anterior:
Passo 4
Agora vamos achar o valor de para o limite do apoio . Vamos achar uma equação que tenha só e como incógnitas, calculando o somatório de momentos em .
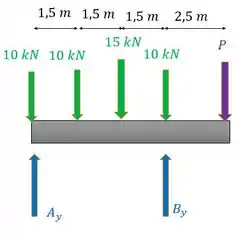
Adotando o sentido anti-horário como positivo teremos
Passo 5
Aí pensa: queremos que o apoio esteja no limite. Então a força que ele suporta é a força limite que suporta. Para achar ela a gente pode usar a expressão da tensão normal admissível de novo:
A força em é e a área do suporte é . E a tensão admissível é . Substituindo essas coisas e isolando :
Podemos substituir na nossa equação do passo anterior:
Como a gente quer o menor valor de entre os dois casos testados, vamos ter que