Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 45
O carregamento distribuído é sustentado pelas três barras de suspensão. e são feitas de alumínio e é feita de aço. Se cada barra tiver área de seção transversal de , determine a intensidade máxima do carregamento distribuído de modo a não ultrapassar uma tensão admissível de no aço e no alumínio. , .
Passo 1
Três barras estão sustentando um carregamento. Há materiais diferentes envolvidos que irão falhar se a tensão das barras for muito alta. Organize primeiro tudo que sabe.
Características das barras :
- Alumínio: , .
- Área transversal: .
- Comprimento inicial: .
- Aço: , .
- Área transversal: .
- Comprimento inicial: .
Características da barra :
O carregamento é distribuído linearmente ao longo de . O que significa que a força equivalente (concentrada) que o carregamento provoca é . Essa força atua no centro de massa: o ponto
Nós queremos achar o valor máximo que pode assumir. O que limita nesse problema é que tem que ser no máximo e tem que ser no máximo .
Passo 2
Monte o diagrama de corpo livre e cheque as condições de equilíbrio.
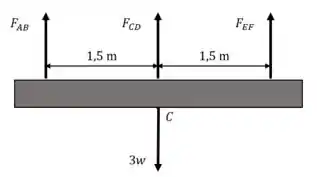
Equilíbrio de momentos ao redor do ponto :
Beleza, então pra simplificar daqui pra frente, vamos dizer que e .
Equilíbrio de forças:
Estamos preocupados com as tensões máximas. Aplique a fórmula da tensão para trabalharmos direto com isso!
Precisamos de uma relação entre as tensões!
Passo 3
Quando uma das barras de alumínio esticar , o comprimento que a barra de aço aumenta tem que ser o mesmo. A condição de compatibilidade é:
Use a fórmula da relação carga-deslocamento:
Use a fórmula da tensão na equação acima:
Daí já sai logo a relação que queremos:
Passo 4
Agora precisamos determinar qual barra (material) falha primeiro. Confira pela última relação.
Caso 1: usando teríamos . OK!
Caso 2: usando teríamos . Não!
Só o Caso 1 é possível, senão a barra de aço falha.
Passo 5
Aplique em , encontrando
Substitua e para acabar
Resposta
Intensidade máxima da carga distribuída: .