Resolver os , usando o círculo de mohr.
Passo 1
Nosso objetivo é determinar as tensões normais e cisalhantes em um estado de tensões que gire 40° no sentido anti-horário e 15° no sentido horário. Sabemos que o nosso elemento é dado por:
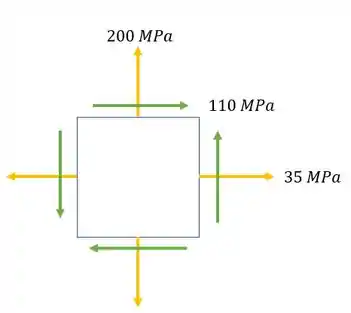
E para determinarmos essas tensões no estado girado pelo círculo de mohr, precisamos lembrar do seguinte:
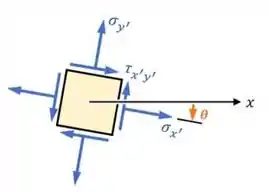

Ou seja, um ângulo que gera uma rotação no sentido horário no estado plano de tensões gera no círculo de mohr o dobro da mesma rotação no sentido anti-horário, e vice versa, com isso já conseguimos pegar o esquema do nosso problema, então vamos ao cálculo.
Passo 2
Sabemos que em seguida, precisamos lembrar que os nossos eixos são dados por duas retas, uma de tensões cisalhantes, e uma de tensões normais:
E sabemos que se juntarmos a tensão x com a negativa da tensão cisalhante e a tensão y com a positiva da tensão cisalhante, obtemos dos pontos pertencentes ao nosso círculo de mohr, e que são imediatamente opostos. Sendo assim teremos que:
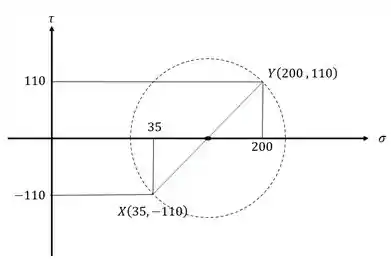
Passo 3
Se ligarmos os pontos, podemos determinar as tensões médias no círculo de mohr:
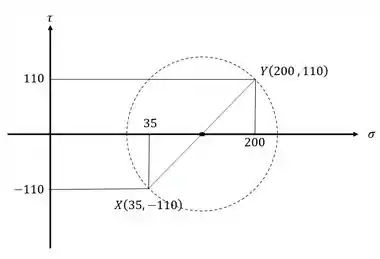
Sabemos que:
Assim podemos determinar também o raio do nosso círculo:

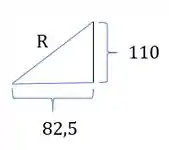
Passo 4
Agora podemos ir pensando os nossos objetivos um por um:
- Determinar os planos principais
- 40° no sentido anti-horário no estado plano de tensões, são 80° no sentido horário no círculo de mohr.
- 15° no sentido horário do estado plano de tensões, representa 30° no sentido anti-horário no círculo de mohr.
Isso podemos ver no nosso círculo da seguinte maneira:

Sabemos que:
Passo 4
Agora vamos lá, precisamos fazer a rotação da nossa seção, sabemos que devemos fazer as seguintes rotações:
Vamos fazer um de cada vez:
- 40° no sentido anti-horário – 80° no sentido horário:
- 15° no sentido horário – 30° no sentido anti-horário:
- 40° no sentido anti-horário
- 15° no sentido horário
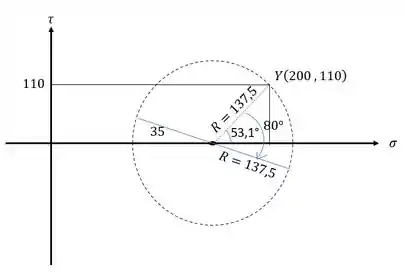
Assim o ângulo com a horizontal formado com relação a nova posição será dado por:

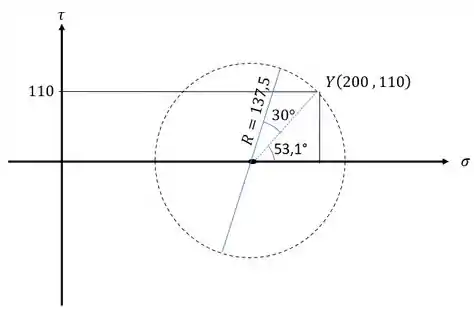
Assim o ângulo com a horizontal formado com relação a nova posição será dado por:

Resposta
Resposta
Ei, a resposta está no passo a passo :)