Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 48
Cada um dos três cabos de aço tem diâmetro de e comprimentos de e quando não carregados. Determine a força em cada cabo depois que a massa de é suspensa pelo anel em .
Passo 1
Uma massa de está puxando três cabos para baixo.
Características do cabo :
- Aço : (Tabelado)
- Comprimento inicial: .
- Diâmetro: .
- Aço : (Tabelado)
- Comprimento inicial: .
- Diâmetro: .
Características dos cabos inclinados ( e ):
O forçamento será o peso de
Queremos a força em cada cabo. A sacada dessa questão é saber usar o ângulo pra decompor forças e enxergar como as deformações interagem
Passo 2
Diagrama de corpo livre.
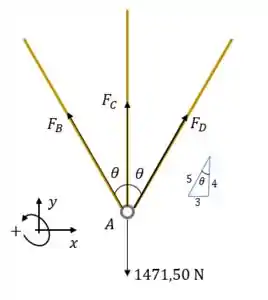
Começamos com as condições de equilíbrio:
Pra facilitar, vamos chamar as forças inclinadas de
Duas incógnitas, vamos precisar de outra equação.
Passo 3
Por causa do peso, as cordas vão ser esticadas (deformação). O ponto vai descer, então em tese o ângulo vai mudar para algum . Mas como estamos sempre assumindo pequenas deformações, essa mudança no ângulo é desprezível: .
Com a aproximação, as retas são praticamente paralelas, e aí o aumento da reta inclinada aparece como na figura acima. Escrevemos
Nessa condição de compatibilidade, o deslocamento é o quanto as cordas inclinadas esticam na direção delas!
Passo 4
Use a fórmula da relação carga-deslocamento
Pelo triângulo , então
Passo 5
Volte à equação resultante do equilíbrio de forças:
Resposta
Força no cabo : . Força nos cabos e : .