Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 24

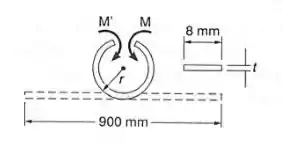
Uma tira de aço de 900 m m de comprimento é encurvada, formando uma circunferência completa, por dois momentos aplicados como mostrado. Determinar:

  1. A máxima espessura t da tira, se a tensão admissível de aço é 420   M P a ;
  2. Os correspondentes momentos M aplicados. Usar E = 200   G P a .

Passo 1

No item a) queremos determinar a máxima espessura da nossa tira, sabemos que a nossa fórmula de tensão admissível é dada por:

σ A D M = E ε m

Dessa fórmula sabemos que:

E = 200   G P a = 200000   M P a

Para determinarmos a máxima deformação, devemos usar a seguinte fórmula:

ε m = c ρ

Substituindo teremos que:

σ A D M = E c ρ

O ρ já e o nosso velho conhecido raio de curvatura, e o raio de curvatura vai usar a nossa formulazinha de comprimento do círculo, sabemos que a equação é dada por:

L = 2 π ρ

Com isso teremos que:

ρ = L 2 π

O comprimento da tira é de 900 m m , sendo assim teremos que:

ρ = 900 2 π = 143,24   m m

Substituindo na fórmula principal, teremos que:

σ A D M = E c ρ

c = σ A D M ρ E

Lembrando que o nosso objetivo é determinar a espessura, e a relação entre C e a espessura, é que o C é o raio da nossa fita, sendo assim teremos que:

c = t 2

Substituindo teremos que:

t 2 = σ A D M ρ E

t = 2 σ A D M ρ E

σ A D M = 420   M P a = 420 N m m 2

ρ = 143,24   m m

E = 200   G P a = 200000   M P a = 200000 N m m 2

t = 2   .   420   .     143,24 200000 = 0,602   m m

Passo 2

No item B) queremos determinar o momento que está agindo na nossa barra. Para isso precisamos lembrar da fórmula que relaciona momento fletor com raio de curvatura, que é dado por:

1 ρ = M E I

Como o objetivo é determinar o momento, usaremos a seguinte conta:

M = E I ρ

Sabemos que:

E = 200   G P a = 200000   M P a

ρ = 143,24   m m

E para o momento de inercia temos que a fita é retangular, sendo assim teremos que:

I = b h 3 12

E sabemos que:

h = t = 0,602

b = 8 m m

I = b h 3 12 = 8   .     0,602 3 12 = 0,145   m m 4

Substituindo teremos que:

M = 200000   N m m 2   .     0,145   m m 4 143,24   m m = 203   N m m = 0,203   N m

Resposta

  1. t = 0,602   m m
  2. M = 0,203   N m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga mostrada na figura é feita de náilon para o qual a tensão admissível é de 24M p a em tração e de 30M p a em compressão. Determine o maior momento fletor M que pode ser aplicado à viga.
Duas forças verticais são aplicadas à viga com a seção transversal mostrada na figura. Determine as tensões de tração e de compressão máximas na parte BC da viga.
Sabendo que a viga de seção transversal mostrada na figura é flexionada em torno do eixo horizontal e que o momento fletor é de 6 k N m , determine a força total que atua na parte sombreada de sua alm
Sabendo que, para a viga mostrada na figura a tensão admissível é de 82,7 Mpa em tração e de 110,3 Mpa em compressão, determine o maior momento fletor M que lhe pode ser aplicado.
Duas forças verticais são aplicadas à viga com a seção transversal mostrada na figura. Determine as tensões de tração e de compressão máximas na parte BC da viga.