Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 22

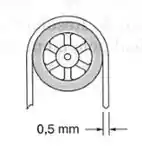
Uma lâmina de aço, que originalmente estava reta, é montada sobre uma serra de fita, que passa sobre polias de de diâmetro. Determinar a máxima tensão na lâmina, sabendo-se que ela tem uma espessura de e uma largura de . Usar .

Passo 1

Queremos determinar a máxima tensão que age na nossa lâmina, sabemos que a nossa fórmula é dada por:

Dessa fórmula sabemos que:

Para determinarmos a máxima deformação, devemos usar a seguinte fórmula:

Sabemos que é o raio da nossa fita, e a espessura da nossa fita é dada por , sendo assim teremos que:

O já e o nosso velho conhecido raio de curvatura, e o raio de curvatura deve englobar tanto o raio da rota quanto o raio da fita, sendo assim teremos que:

Substituindo na nossa deformação teremos que:

E substituindo na nossa fórmula de tensão teremos que:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um conjunto de 60 N m é aplicado à barra de aço mostrada.Admitindo que o conjunto é aplicado na direção do eixo z conforme mostrado, determine a tensão máxima e o raio de curvatura da barra.Resolva a

Sabendo que, para a viga extrudada mostrada na figura, a tensão admissível é de 120 M P a em tração e de 150M P a em compressão, determine o maior momento fletor M que lhe pode ser aplicado.

Hastes retas com 0,3 0 i n de diâmetro e 200 f t de comprimento são utilizadas algumas vezes para desobstruir dutos enterrados ou para passar cabos em dutos novos. As hastes são feitas de aço de alta

Utilizando a tensão admissível de 120M p a , determine o maior conjugado M que pode ser aplicado à viga cuja seção transversal é a mostrada.Resolva a parte a, admitindo que a seção transversal da viga

Sabendo que, para a viga mostrada na figura a tensão admissível é de 82,7M P a em tração e de 110,3M p a em compressão, determine o maior momento fletor M que lhe pode ser aplicado.