Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 10

Duas forças verticais são aplicadas à viga com a seção transversal mostrada na figura. Determine as tensões de tração e de compressão máximas na parte BC da viga.

Passo 1

Nosso objetivo é determinar os momentos fletores, e a fórmula que relaciona a tensão com o momento é dado por:

σ x = - M y I

Como não temos a LN da nossa barra, precisamos determinar ela. Isso é de suma importância para podermos fazer toda a conta, por isso precisamos seguir um passo a passo para determinar a LN.

Para isso precisamos dividir a nossa seção em seções mais simples (sempre que for possível precisamos fazer seções retangulares) e determinar a distância do centroide de cada seção até a base da peça total, assim, temos que:

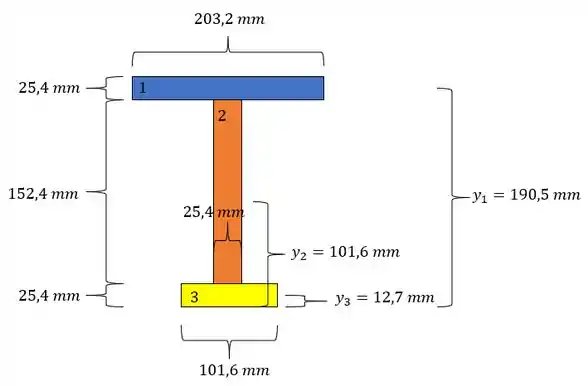
Agora para termos a linha neutra basta fazermos o seguinte:

y - = A 1 y 1 + A 2 y 2 + A 3 y 3 A 1 + A 2 + A 3

Assim temos que:

A 1 = 203,2 × 25,4 = 5161,28   m m 2

A 2 = 152,4 × 25,4 = 3870,96   m m 2

A 3 = 101,6 × 25,4 = 2580,64   m m 2

y 1 = 190,5   m m

y 2 = 101,6   m m

y 3 = 12,7   m m

y - = 5161,28 × 190,5 + 3870,96 × 101,6 + 2580,64 × 12,7 5161,28 + 3870,96 + 2580,64 = 121,36   m m

Assim a nossa LN é:

Passo 2

Agora que temos a LN, podemos determinar o momento de inércia, e o momento de inércia vai ser dado pela seguinte equação:

I = I 1 + I 2 + I 3 + ( A 1 d 1 2 + A 2 d 2 2 + A 3 d 3 2 )

Em que as áreas já definimos no passo anterior, e os valores de I 1   , I 2   e   I 3 são os momentos de inércia de cada uma das seções mais simples. E d 1 ,   d 2   e   d 3 são as distâncias do centroide de cada uma das peças mais simples até a LN, assim as medidas da nossa seção são dadas abaixo.

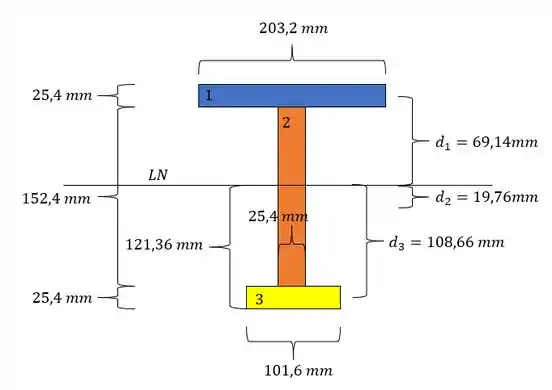
Além disso temos que:

I 1 = b h 3 12 = 203,2 × 25,4 3 12 = 277487,6   m m 4

I 2 = b h 3 12 = 25,4 × 152,4 3 12 = 7492165,7   m m 4

I 3 = b h 3 12 = 101,6 × 25,4 3 12 = 138743,8   m m 4

Assim a inercia da nossa seção vai ser dada por:

I = 277487,6 + 7492165,7 + 138743,8 + ( 5161,28 × 69,14 2 + 3870,96 × 19,76 2 + 2580,64 × 108,66 2 )

I = 64562119,2   m m 4

Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.

Passo 3

O valor de y é a distância da LN para as extremidades, assim teremos que:

  • y - positivo e negativo

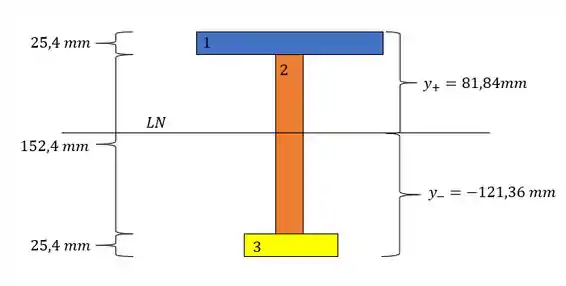
para o momento fletor é bem tranquilo, como as cargas são simétricas, basta somarmos as duas e dividir por dois que teremos as reações de apoio, e tendo a reação de apoio conseguimos determinar o momento atuante no centro da viga, fazendo isso, teremos que:

M + 111,2 × 762 - 111,2 × 1270 = 0

M = 56489,6   k N m m

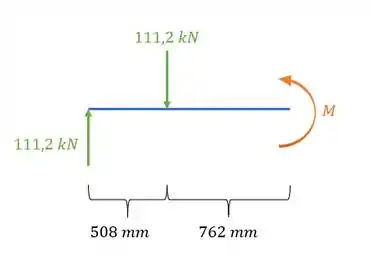
Ou seja, o nosso momento traciona as fibras da parte de baixo, ou seja, o momento é positivo. Se traciona a parte de baixo sabemos que a tensão é positiva, sendo assim teremos que:

y - = - 121,36   m m

I = 64562119,2   m m 4

M = 56489,6   k N m m

σ x = - M y I

Substituindo, teremos que:

σ t r a ç ã o = - 56489,6   k N m m × - 121,36 [ m m ] 64562119,2   [ m m 4 ]

σ t r a ç ã o = 0,1062 k N m m 2 = 106,2   M P a

E analisando agora a compressão teremos que:

y + = 81,84 m m

I = 64562119,2   m m 4

M = 56489,6   k N m m

σ x = - M y I

Substituindo, teremos que:

σ c o m p r e s s ã o = - 56489,6   k N m m × 81,84 [ m m ] 64562119,2   [ m m 4 ]

σ c o m p r e s s ã o = - 0,0716 k N m m 2 = - 71,6   M P a

Resposta

σ t r a ç ã o = 106,2   M P a

σ c o m p r e s s ã o = - 71,6   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga do problema 78, um momento igual ao momento plástico Mp da viga é aplicado e, depois, removido. Usando uma tensão de escoamento de 300MPa, determinar a tensão residual para y1 = 24mm e y2
Um momento M é aplicado à viga do problema 77, em torno do eixo z, causando zonas plásticas de 25 mm de espessura na parte superior e inferior da viga. Depois do momento ser removido determinar: (a) a
Determinar o momento plástico Mp, de uma viga de aço de seção transversal mostrada,quando a viga é encurvada em torno do eixo horizontal. Assumir que o aço é elastoplástico, com uma tensão de escoamen
Considerando a viga do problema 76, é aplicado um momento igual ao momento plástico Mp da viga e, depois removido. Usando uma tensão de escoamento de 290 MPa, determinar a tensão residual para y1 = 25
Um momento M é aplicado à viga do problema 76, em torno do eixo z, causando zonas plásticas de 25 mm de espessura na parte superior e inferior da viga. Depois do momento ser removido determinar: (a) a