Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 98
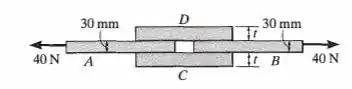
As tiras e devem ser colocadas com a utilização das duas tiras e . Determine a espessura exigida para e de modo que todas as tiras falhem simultaneamente. A largura das tiras e é vez a das tiras .
Passo 1
Desejamos dimensionar as tiras de e que possuem comprimento igual a . Como ele quer que todas as tiras falhem simultaneamente devemos ter que as seguintes condições sejam satisfeitas
Lembrando que a tensão normal média é dada por
Sendo a força normal que atua no problema;
Passo 2
Tomemos a seguinte construção para entendermos o problema e a formulação das igualdades
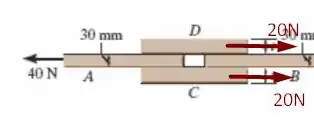
Dessa forma, vamos ter
Pelo enunciado temos que a largura das tiras e é vez a das tiras .Assim, e vamos obter
Resposta
Exercícios de Livros Relacionados
Para o estado de tensões dado, determinar as tensões, normais e de cisalhamento, exercidas sobre a face obliqua do triângulo sombreado do elemento. Usar o método de análise baseado nas equações de equ
Para o estado de tensões dado, determinar as tensões, normais e de cisalhamento, exercidas sobre a face obliqua do triângulo sombreado do elemento. Usar o método de análise baseado nas equações de equ
Para o estado de tensões dado, determinar as tensões, normais e de cisalhamento, exercidas sobre a face obliqua do triângulo sombreado do elemento. Usar o método de análise baseado nas equações de equ
Para o estado de tensões dado, determinar:Os planos principais;As tensões principais.
Para o estado de tensões dado, determinar:Os planos principais;As tensões principais.