Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 36
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
Passo 1
Fala galerinha bonita, tudo beleza?
Vamos, primeiramente, utilizar as equações de equilíbrio para determinarmos as reações de apoio:
Logo será:
Agora para faremos:
Tal que:
Belezoca, agora que a gente já tem os valores das forças, podemos escrever as equações do esforços internos, bora lá!
Passo 2
Show de bola, então se a gente dividir a viga em seções, vamos obter que:
Seção 1, no intervalo , vamos obter que:
E do mesmo modo:
Logo:
Agora para a Seção 2, no intervalo , vamos descobrir que
Dessa maneira, será:
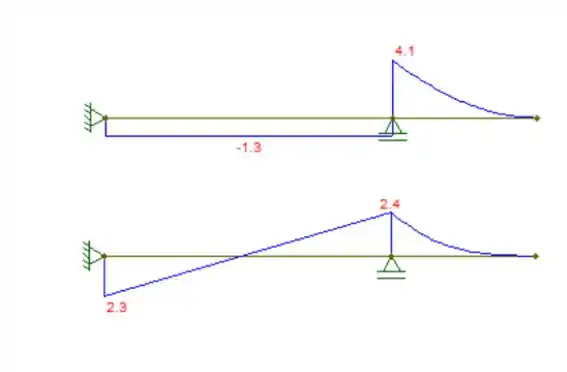
Com as reações calculadas, podemos fazer os diagramas de cortante e momento fletor, respectivamente:
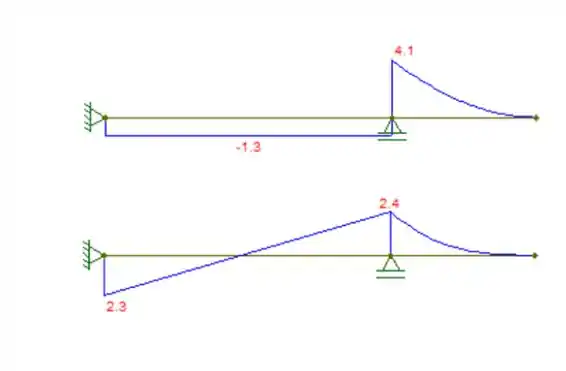
Resposta
Exercícios de Livros Relacionados
A viga mestra A B suporta a carga na asa do avião. As cargas consideradas são a reação da roda de 175k N em C , o peso de 6k N do combustível no tanque da asa, com centro de gravidade em D, e o peso d
O cano tem massa de 12k g / m . Se ele estiver fixado à parede em A , determine as cargas internas resultantes que agem na seção transversal em B . Despreze o peso da chave C D .
Determine as cargas internas resultantes nas seções transversais que passam pelos pontos K e J no guindaste de tambores no Problema 1. 21.
O guindaste de tambores suspende o tambor de 2,5k N . O pino de ligação está conectado à chapa em A e B . A ação de aperto sobre a borda do tambor é tal que somente forças horizontais e verticais são
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto D no Problema 1. 18.