Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 4

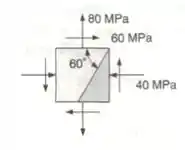
Para o estado de tensões dado, determinar as tensões, normais e de cisalhamento, exercidas sobre a face obliqua do triângulo sombreado do elemento. Usar o método de análise baseado nas equações de equilíbrio deste elemento, tal como foi deduzido na S e c . 6.2 .

Passo 1

Então galerinha, vamos pegar os macetes desse exercício para ficar mais fácil resolver qualquer exercício que encontrarmos sobre isso.

O nosso objetivo é determinar as tensões em um estado que a nossa nova posição seja paralela ao plano de tensões que desejamos saber as tensões, pode parecer meio estranho, mas vamos ver o desenho abaixo pra ficar mais fácil de entender:

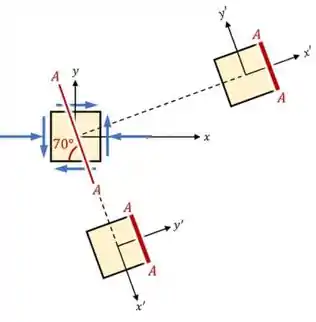
Se fizermos a mesma analise para o nosso caso, teremos que:

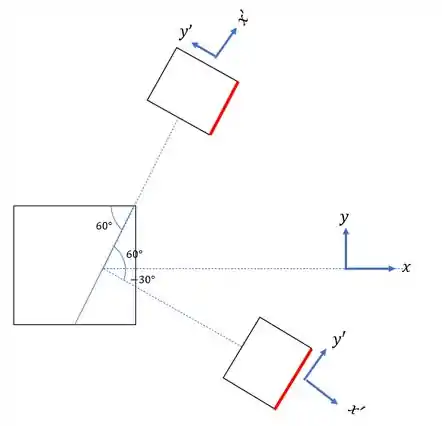
Perceba que os dois estados finais possíveis tem seções paralelas, e perceba que girar para baixo significa ter um ângulo de giro negativo, e se girar pra cima, significa ter um ângulo de giro positivo, isso era o mais difícil da nossa fórmula, que é a determinação dos ângulos, agora só precisamos lembrar que o elementos básicos é dado por:

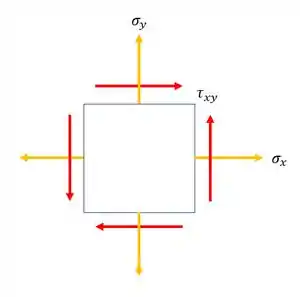
Como o nosso elemento é dado por:

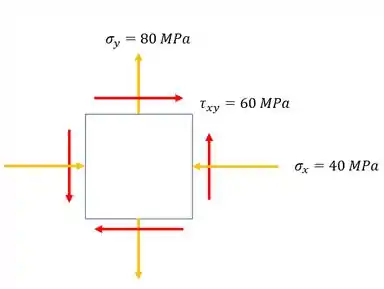
Com isso teremos que:

σ x = - 40   M P a

σ y = 80   M P a

τ x y = 60   M P a

θ = 60 °   o u - 30 °

Passo 2

Agora que já temos todos os dados, precisamos apenas das fórmulas, com as fórmulas, teremos as tensões que precisamos, sendo assim, teremos que:

σ x ' = σ x + σ y 2 + σ x - σ y 2 C O S 2 θ + τ x y S E N 2 θ

σ y ' = σ x + σ y 2 - σ x - σ y 2 C O S 2 θ - τ x y S E N 2 θ

τ x ' y ' = - σ x - σ y 2 S E N 2 θ + τ x y C O S 2 θ

Substituindo os nossos dados a 60°, teremos que:

σ x ' = - 40 + ( 80 ) 2 + - 40 - ( 80 ) 2 C O S 2   .     60 + 60 .     S E N 2   . 60 = 101,96   M P a

σ y ' = - 40 + ( 80 ) 2 - - 40 - 80 2 C O S 2   .     60 - 60 .     S E N 2   . 60 = - 61,96   M P a

τ x ' y ' = - - 40 - 80 2 S E N 2   .     60 + 60 .   C O S 2   .   60 = 21,96   M P a

Substituindo os nossos dados a -30°, teremos que:

σ x ' = - 40 + ( 80 ) 2 + - 40 - ( 80 ) 2 C O S 2   .   - 30 + 60 .     S E N 2   . - 30 = - 61,96   M P a

σ y ' = - 40 + ( 80 ) 2 - - 40 - 80 2 C O S 2   .   - 30 - 60 .     S E N 2   . - 30 = 101,96   M P a

τ x ' y ' = - - 40 - 80 2 S E N 2   .   - 30 + 60 .   C O S 2   .   - 30 = - 21,96   M P a

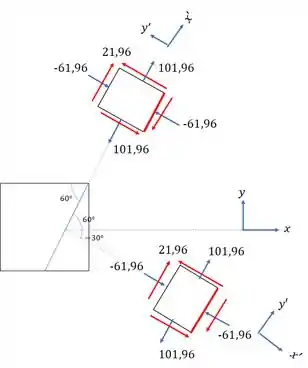
Com isso as nossas seções serão dadas por:

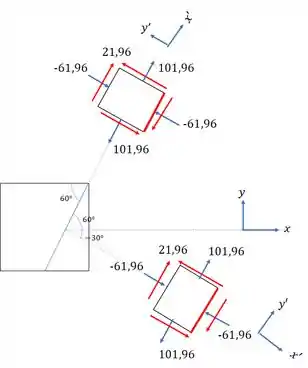
Bora pra próxima questão porque essa já ta feita, vamos nessa?

Resposta

Substituindo os nossos dados a 60°, teremos que:

σ x ' = 101,96   M P a

σ y ' = - 61,96   M P a

τ x ' y ' = 21,96   M P a

Substituindo os nossos dados a -30°, teremos que:

σ x ' = - 61,96   M P a

σ y ' = 101,96   M P a

τ x ' y ' = - 21,96   M P a

Com isso as nossas seções serão dadas por:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga A B tem uma seção transversal retangular de largura b constante e a altura h variável. Sabendo-se que a viga deve ser de resistência constante, expressar h , em termos de x ,L e h 0 .
Resolver o Prob. 7.113, assumindo que a distância a é mudada para 0,55m .
Para a viga com o carregamento mostrado, determinar a largura b da viga e a distância x , para que a tensão normal máxima σ m e a tensão máxima de cisalhamento τ m na viga sejam simultaneamento iguais
Para a viga com o carregamento mostrado, determinar a largura b da viga e a distância x , para que a tensão normal máxima σ m e a tensão máxima de cisalhamento τ m na viga sejam simultaneamento iguais
Usando a equação derivada da parte b do Prob. 7.126, mostrar que, em qualquer seção transversal da viga da Fig. 7.24, onde x ≥ 0,5444c , o maior valor de σ m á x á ocorre para y = c . (Sugestão: Denot