Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 52
Trace os diagramas de cortante e momento fletor e determine os valores máximos absolutos dos esforços na estrutura a seguir.
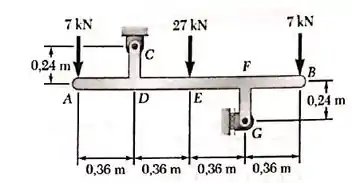
Passo 1
Fala aí galera, vamos para mais um problema de estática. Para traçar os diagramas, primeiro devemos aplicar as equações de equilíbrio para determinar as reações de apoio.
Aplicando as equações para a barra, teremos:
Logo, fazendo os diagramas:
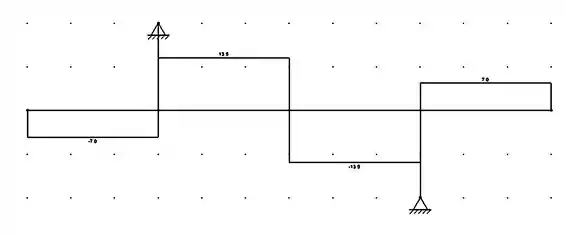
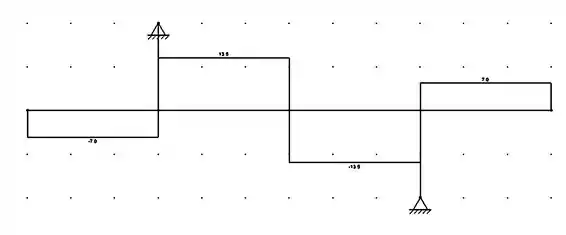
Passo 2
Como podemos ver no diagrama, os valores máximos absolutos dos esforços na viga serão serão:
Resposta
Exercícios de Livros Relacionados
A viga uniforme é levada por cabos de guindaste ligados em A e B. Determine a distância a das extremidades da viga ate os pontos onde os cabos devem ser ligados se o máximo valor absoluto do momento f
Duas cargas estão suspensas no cabo A B C D tal como mostra a figura. Sabendo que h B = 1,8m , determine a a distância h C , b os componentes da reação em D , c a tração máxima do cabo.
Resolva o Problema 7.60 considerando que P = 1350N e Q = 675N ..
Se d C = 2,4m , determine a a reação A , b a reação E .
Para reduzir o momento fletor na viga em balanço A B , um cabo e um contrapeso são permanentemente ligados à extremidade B . Determine o valor do contrapeso para o qual o valor absoluto máximo do mome