A viga uniforme é levada por cabos de guindaste ligados em A e B. Determine a distância das extremidades da viga ate os pontos onde os cabos devem ser ligados se o máximo valor absoluto do momento fletor é o menor possível (Dica: trace o diagrama de momento fletor em termos de e o peso por unidade de comprimento, e depois iguale os valores absolutos dos maiores momentos fletores positivo e negativo obtidos.)
Figura P7.58
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiramente é importante perceber a simetria da aplicação das forças atuando na viga em relação a um eixo vertical que passa pelo centro dela. Isso facilita a análise e elaboração dos gráficos de força cortante e momento fletor, pois pode levar a gráficos com certa simetria também em relação a esse mesmo eixo.
Passo 2
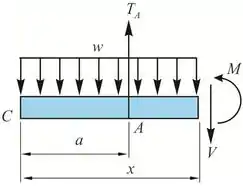
Monte o diagrama de corpo livre da viga:

Passo 3
No diagrama de corpo livre, e representam a tração nos cabos A e B, respectivamente, representa o peso por unidade de comprimento e representa o comprimento da viga. E também devido a simetria, . Podemos encontrar a força de tração nos cabos usando a equação de equilíbrio na direção y.
Substituindo por :
Passo 4
Por hora, de acordo com o enunciado, não será necessário a elaboração do gráfico de força cortante. Assim, vamos calcular apenas o gráfico de momento fletor. Para isso, considere a seção entre CA a uma distancia de C.

Encontramos o momento fletor na seção calculando:
......................................(Eq. 1)
Calcule o momento fletor no ponto C, substituindo por 0 na Eq. 1.
Calcule o momento fletor no ponto A, substituindo por na Eq. 1.
Passo 5
Agora vamos considerar a seção AB a uma distancia do ponto C.
Calcule o momento fletor na seção:
.................................(Eq. 2)
Passo 6
Como citado anteriormente, devido a simetria da viga, agora podemos construir o diagrama de momento fletor da viga, pois obtemos as equações das principais seções (Eq.1 e Eq. 2).
Calculando o momento fletor no ponto :
Passo 7
Monte o diagrama de momento fletor.
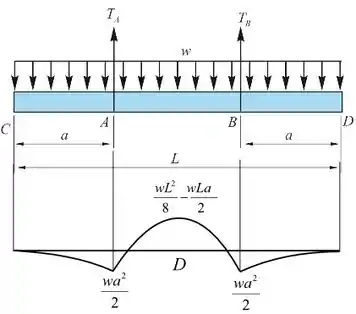
Passo 8
Seguindo a recomendação do enunciado da questão, temos que:
maxA
Resolva a equação do segundo grau.
Resposta
A distancia da extremidade da viga ate onde os cabos devem ser ancorados é: