Um tubo de latão de de comprimento, com de diâmetro externo e de espessura, é fixado em um torno mecânico manual, que está ajustado de tal modo que os mordentes encostem nas suas extremidades, sem que exerça qualquer pressão nessas. Duas forças e , de intensidade e , são então aplicadas ao tubo, como indicado. Após as forças serem aplicadas o torno é ajustado com um amento da distância entre os mordentes de . Sabendo-se que , determinar: (a) as forças exercidas pelo torno sobre o tubo em e ; (b) a elongação da parte do tubo.
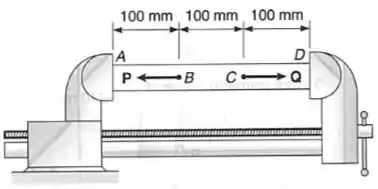
Passo 1
Estamos diante de um problema estaticamente indeterminado, logo a solução através apenas das forças é impossível, por isso que vamos ter de utilizar as equações de deslocamento também.
Então o nosso objetivo aqui é utilizar o somatório das forças na horizontal e o deslocamento da barra para acharmos, tanto as forças de reação quanto as deflexões, neste caso a deflexão total será igual a .
Perceba que, por causa do ajuste, o agora vale , que é exatamente a “frouxidão” deixada pelo ajuste.
Passo 2
Fazer o diagrama de corpo livre do tubo, de modo a achar uma equação com as forças de reação:
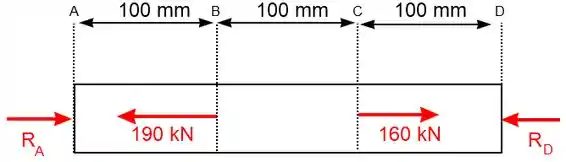
Onde e são as reações de apoio que o tubo sofre. lembrando que estes sentidos sempre serão arbitrários, caso estejam corretos, ao final do exercício iremos achar valores positivos, caso estejam errados acharemos valores negativos.
Como a barra está estática podemos afirmar que:
Lembrando que é sempre importante decidir um sentido positivo e carrega-lo até o fim do exercício! Aqui vamos escolher o sentido que aponta para a direita como positivo.
Passo 3
Como vimos o problema está estaticamente indeterminado e precisamos achar uma outra equação para podermos achar as reações e . Essa outra equação é a da deflexão.
Para o nosso caso temos 3 partes, ou 3 deltas (), então nossa equação fica da forma:
Nós temos quase todos os dados, temos o tamanho inicial , a área e o coeficiente de elasticidade . Porém, não temos as forças . Para achar essas forças temos que cortar cada pedaço (AB, BC e CD) e ver quais forças estão aplicadas apenas nesse pedacinho cortado, como mostrado no próximo passo.
Passo 4
- Para o segmento AB:
- Para o segmento BC:
- Para o segmento CD

Então a força aplicada no segmento AB é igual a negativo.
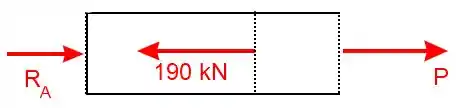
Repare que aqui, para que a força mantenha o corpo em equilíbrio ela deve ser igual a

Aqui deve ser igual a
Aqui vale uma observação!
Neste caso fomos seccionando a barra da esquerda para a direita e repare que não apareceu, poderíamos fazer da direita para a esquerda também. Ainda mais, poderíamos pegar apenas a última parte da direita para a esquerda e o resto da esquerda para a direita.
Ou seja, o método de seccionar a barra não importa, o que importa é manter sempre os mesmos sentidos.
Passo 5
Agora vamos voltar para nossa equação do deslocamento e aplicar os valores, já que conhecemos todos agora (pelo menos em função de né!? Que é o que queremos)
Lembrando que a área neste caso será calculada como um círculo menos o outro, um com de diâmetro e o outro com , os comprimentos são todos iguais a e o coeficiente de elasticidade é igual a .
Dividindo ambos os lados da equação por
Perceba que o valor deu negativo logo a força aponta, na verdade, para a esquerda!
Passo 6
Agora substituímos na equação lá do passo 2:
Aqui a força também deu negativa logo, na realidade, é oposta ao que imaginamos inicialmente
E voilà a letra A morreu
Onde aponta para a esquerda e para a direita!
Passo 7
Agora para responder a letra b basta aplicar a equação do deslocamento novamente, da seguinte forma.
Perceba que, como fizemos todo os desenvolvimento assumindo um sentido, devemos continuar utilizando este mesmo sentido! Por isso o acaba ficando positivo.
Obs: Só na hora da resposta que fica mais ELEGANTE kkk utilizar o módulo e, possivelmente indicar o sentido, se necessário.
É legal perceber que quando utilizamos a força em , o comprimento em , a área em e o módulo de elasticidade em , o nosso resultado aparece em .
Resposta
a)
b)