Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 52
Resolver o , assumindo que a estrutura deve ser reprojetada para utilizar pinos de de diâmetro em A e C, assim como também em B, e que nenhuma outra modificação deve ser feita.
Passo 1
Essa questão é bem interessante, e por isso precisamos tomar bastante cuidado com ela. Sabemos pelo enunciado os seguintes dados:
Se temos os diâmetros e áreas das seções, assim como as tensões resistentes, podemos determinar a força máxima que cada seção pode suportar usando a seguinte equação:
Em que queremos determinar a força, sendo assim teremos que:
Fazendo isso para todas as nossas estruturas teremos que:
- O pino em B é normal, logo usamos a nossa fórmula normalmente também.
- Pino em A
- Barra AC
- Pino em B
- Pino em A
- Barra AC
- Pino em B
- Pino em A que também vai dar os esforços da barra AC
- Pino em B
- Pino em A
- Barra AC
O pino em A é normal, logo usamos a nossa fórmula normalmente também.
Esse tem uma peculiaridade que é tirarmos da seção solicitada a área do parafuso, ou seja, se temos um parafuso de 9,5 mm em uma chapa de espessura 6mm, precisamos descontar essa área na resistência, logo usamos a nossa fórmula, teremos:
Mas vale lembrar que queremos um fator de segurança de 3,25 , e sabemos que podemos escrever a nossa fórmula com o fator de segurança da seguinte maneira:
Como queremos a força aplicada podemos definir como:
Calculando para cada pino teremos que:
Ou seja, agora já sabemos as forças que as estruturas suportam.
Passo 2
Para sabermos quanto age em cada estrutura precisamos determinar o valor das reações de apoio, e para isso precisamos olhar a nossa estrutura:
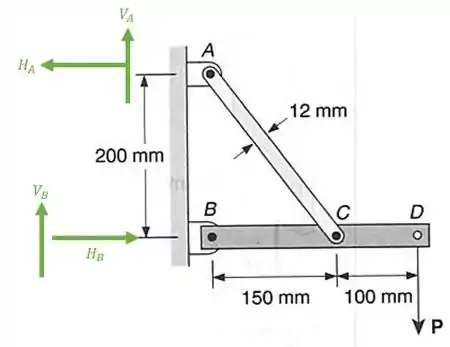
Olha que macete legal, que a barra AC está ligada por pinas a barra BCD, e como no enunciado diz que no ponto C não tem nenhum tipo de reforço, então podemos concluir que não há transferência de momentos fletores entres as barras. Ou seja, se eu fizer um somatório de momentos no ponto C vindo a partir do ponto A, esse somatório de momentos tem que dar zero, porque pensa só, se a barra AC pode girar em trono do parafuso C, então ali não temos momento fletor, fazendo isso teremos que:
Fazendo agora o somatório de momentos no ponto A teremos que:
Com isso encontramos que:
E sabendo conseguimos saber quanto vale , que é dado pela equação do primeiro somatório.
Para calcular fazemos o somatório de forças verticais:
Agora precisamos definir qual a carga máxima que age nos pinos e na barra, para isso precisamos somar os vetores de cada um dos pinos, com isso teremos que:
As forças que agem no pino em B são:
Como nosso objetivo é determinar a força em P, podemos fazer:
As forças que agem no pino em A são:
Como nosso objetivo é determinar a força em P, podemos fazer:
Passo 3
Verificando as estruturas teremos que:
E agora é simples, a carga que deve ser aplicada para respeitar as condições impostas pelo problema é aquela que for a menor entre as verificadas, além do mais, qualquer carga que for maior vai romper o elo mais fraco, enquanto a carga menor garante o elo mais fraco e não afeta os mais fortes, sendo assim a carga que deve ser usada é: