Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 56

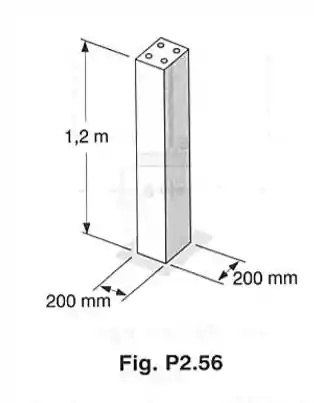
Uma coluna de concreto de 1,2   m é reforçada por quatro barras de aço, cada uma de 20   m m de diâmetro, como indicado. Sabendo-se que para o aço E = 200   G P a e α = 11,7 × 10 - 6 / ° C e para o concreto E = 25 G P a e α = 9,9 × 10 - 6 / ° C , determinar as tensões normais induzidas no aço e no concreto, devidas a um aumento de temperatura de 27°C.

Passo 1

Neste exercício podemos ver que, devido ao aumento de temperatura, haverá uma dilatação do aço e do concreto. Além disso, o aço dilatará mais do que o concreto, fazendo assim com que o concreto sofra tensões de tração (enquanto o concreto, por sua vez, exerce tensões compressivas ao aço).

O mais importante aqui é reparar que a variação e comprimento, tanto do aço quanto do concreto, serão iguais e ambas dependem da dilatação térmica e da deflexão pelas tensões. O que podemos expressar como:

δ = δ T C + δ C = δ T A - δ A

Onde

  • δ T C é a dilatação térmica do concreto.
  • δ C é a deflexão do concreto causada pela tensão trativa.
  • δ T A é a dilatação térmica do aço.
  • δ A é a deflexão do aço causada pela tensão compressiva.

Passo 2

Vamos calcular então as dilatações térmicas, primeiro para o aço:

δ T A = α ⋅ L ⋅ Δ T

δ T A = 11,7 × 10 - 6 ⋅ 1,2 ⋅ 27

δ T A = 379,08 × 10 - 6 m

δ T A = 379,08 × 10 - 3 m m

δ T A = 0 , 37908   m m

Para o concreto

δ T C = α ⋅ L ⋅ Δ T

δ T C = 9,9 × 10 - 6 ⋅ 1,2 ⋅ 27

δ T C = 320,76 × 10 - 6 m

δ T C = 320,76 × 10 - 3   m m

δ T C = 0,320 76   m m

Passo 3

Agora as deflexões devido às tensões, primeiro para o concreto:

δ C = F ⋅ L A ⋅ E

δ C = F ⋅ 1200 ( 200 × 200 ) ⋅ 25

δ C = 1,2 × 10 - 3 ⋅ F

Para o aço

δ A = F ⋅ L A ⋅ E

A área das barras de aço é igual a, lembrando que são 4

A = 4 ⋅ π ⋅ D ² 4

A = π ⋅ D ²

A = π ⋅ 20 ²

A = 1256,63   m m ²

δ A = F ⋅ 1200 1256,63 ⋅ 200

δ A = 4,77 × 10 - 3 ⋅ F

Passo 4

Agora vamos colocar tudo na fórmula que a gente tem, lá no início

δ T C + δ C = δ T A - δ A

0,32076 + 1,2 × 10 - 3 ⋅ F = 0,37908 - 4,77 × 10 - 3 ⋅ F

Resolvendo

4,77 × 10 - 3 ⋅ F + 1,2 × 10 - 3 ⋅ F = 0,37908 - 0,32076

( 4,77 + 1,2 ) × 10 - 3 ⋅ F = 0,37908 - 0,32076

5,97 × 10 - 3 ⋅ F = 0 , 05832

F = 0,05832 5,97 ⋅ 10 3   k N

F = 9,77   k N

Passo 5

A tensão induzida será de:

A) Para o aço

σ A = F A

σ A = 9770 1256,63

σ A = 7,77   M P a

B) Para o concreto

σ C = F A

σ C = 9770 40000

σ C = 0,24   M P a

Resposta

σ A = 7,77   M P a

σ C = 0,24   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o P r o b .1.50 , assumindo que a estrutura deve ser reprojetada para utilizar pinos de 12 m m de diâmetro em B e D , e que nenhuma outra modificação deve ser feita.
Um fio de Nylon está sujeito a uma tração de 9,0 N . Sabendo-se que E = 3,45G P a e que a máxima tensão normal admissível é de 40M P a , determinar:O diâmetro necessário para o fio;O correspondente ac
Uma haste de controle feita de latão-amarelo deve alongar-se de 3,2 m m , quando sujeito a uma carga de 4000 N . Sabendo-se que E = 105 G P a e que a máxima tensão normal admissível é de 415M P a , de
Uma haste de poliestireno, de comprimento 300 m m e diâmetro 25,4m m , é submetida a uma carga de tração de 3560N . Sabendo-se que E = 3,1G P a , determinar:O alongamento da haste.A tensão normal na h
Num arame de alumínio de 4 m m de diâmetro, é observado um alongamento de 25 m m , quando a tração no arame é de 400 N . Sabendo-se que E = 70 G P a e, que a tensão última para o alumínio é de 110M P