Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 11
Um tubo de madeira com diâmetro interno de 0,9 m é atado com aros de aço cuja área de seção transversal é 125 mm². Se a tensão admissível para os aros for σadm = 84 MPa, determine o espaçamento máximo s dos aros ao longo da seção do tubo de modo que este possa resistir a uma pressão manométrica interna de 28 kPa. Considere que cada aro suporta a pressão do carregamento que age ao longo do comprimento s do tubo.
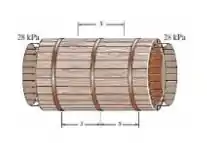
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que o nosso barril tem aros de125 mm² e tensão de 84MPa, distando de s e fazendo a mesma força de tração, sendo que o barril tem 0,45 m de raio interno. Depois de falar isso tudo, ele nos pede a distância s e a força de cada aro. Viu?? Nem é tão difícil assim. Bora lá fazer?? Partiu??
Passo 2
Nosso primeiro passo será determinar qual a força exercida pela água.
Passo 3
Com isso, podemos fazer que a soma das forças internas é zero, achando, assim, a força em cada aro e a distância s.