Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 79

Resolva o problema 8.78 se a seção transversal for quadrada de dimensões 6mm por 6mm

Passo 1

Dados da questão: P = 250   N ,   b = 6 m m ,   h = 6 m m ,   r = 30 m m

A questão pede a tensão de tração e de compressão sobre a seção transversal.

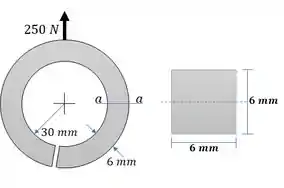
Por conveniência vamos calcular logo o raio externo e o raio central:

r 0 = r + b ⇒ r 0 = 36   m m

r - = r + b 2 ⇒ r - = 33   m m

Passo 2

Vamos calcular as propriedades geométricas da seção de acordo com a tabela 6.2

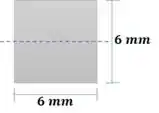
A área da seção:

A = b h ⇒ A = 36   m m 2

O momento de inércia de viga curva:

∫ A d A r = b ⋅ ln ⁡ r 0 r

∫ A d A r = 6 ⋅ ln ⁡ 36 30

∫ A d A r = 1,0939   m m

O raio de curvatura:

R = A ∫ A d A r ⇒ R = 32,9 09   m m

Passo 3

Vamos fazer uma seção na região de interesse a calcular os esforços interno:

∑ F y = 0 ⇒ 250 - F R = 0 ⇒ F R = 250   N

∑ M = 0 ⇒ - F R ⋅ R + M = 0

M = 8227 , 2 5   N ⋅ m m

Passo 4

Agora vamos calcular a tensão gerada pela força.

σ N = F R A

σ N = 250   N 36   m m

σ N = 6,94   M P a

Note que a tensão normal é tração

Passo 5

Vamos calcular a tensão gerada pelo momento no ponto interno da seção:

σ = σ N + M ( R - r ) A ⋅ r ⋅ ( r - - R )

Aplicando os valores

σ = 6,94 + 8227,5   N ⋅ m m ⋅ ( 32,9 09     m m - 3 0   m m ) 36   m m 2 ⋅ 3 0   m m ⋅ ( 33   m m - 32,909     m m )

σ = 250,47   M P a

Passo 6

Vamos calcular a tensão gerada pelo momento no ponto externo:

σ 0 = σ N + M ( R - r 0 ) A ⋅ r 0 ⋅ ( r - - R )

Aplicando os valores

σ 0 = 6,94 + 8227,5   N ⋅ m m ⋅ ( 32,91     m m - 36   m m ) 36   m m 2 ⋅ 36   m m ⋅ ( 33   m m - 32,91     m m )

σ 0 = - 2 08,69   M P a

Resposta

σ = 25 0,47   M P a

σ 0 = - 2 08,69   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

β = 0) e com seu eixo longitudinal AB horizontal, determine a intensidade da força P para a qual a tensão normal no ponto a é +120Mpa, (b) Resolva a parte a considerando que a viga é instalado com β =
Quatro forças são aplicadas a um perfil de aço laminado W8 x 28, conforme mostra a figura. Determine as tensões principais e a tensão de cisalhamento máxima no ponto b.
P 1 e P 2 são aplicadas, como mostrado na figura, em direções perpendiculares ao eixo longitudinal de uma viga W310x60. Sabendo que P 1 = 25 k N e P 2 = 24 k N , determine as tenções principais e a te
Desprezando o efeito dos adoçamentos e das concentrações de tensões, determine os menores diâmetros permissíveis para as hastes sólidas BC e CD. Utilize T a d m = 60 M P a .
a) Sabendo que σ a d m = 165,5 M P aeτ a d m = 100 M P a , selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar o carregamento mostrado. (b) Determine os valores a se