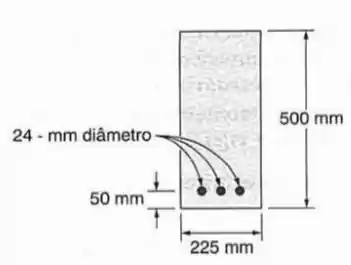
Uma viga de concreto é reforçada por três barras de aço, colocadas como indicado. Os módulos de elasticidade são para o concreto e de para o aço. Usando uma tensão admissível de para o concreto e de para o aço, determinar o maior momento fletor que pode ser aplicado à viga.

O cálculo da seção transformada é feito da seguinte maneira, sabendo que a viga é encurvada no eixo horizontal.

Observe que existe uma parte em branco! É exatamente onde o concreto está sob tensão, como o concreto não resiste a esse tipo de esforço então consideramos que não há material ali.

Atenção aqui a área da viga é igual a:

Calculando

Essa informação não foi dada no problema mas pode ser retirada da tabela no final do livro.

Sendo assim a área que iremos considerar será:

Observe que a linha central (com traços e pontos) está representando o eixo por onde a a viga é encurvada.

Pronto! Temos a seção transformada (toda em concreto no caso). Agora vamos calcular o momento de inércia desta seção no passo 3.

O momento de inércia é calculado normalmente, para seções retangulares, da forma:

Como a linha neutra da seção transversal passa pelo centroide da seção transformada vamos utilizar a seguinte equação:

Onde os valores são representados abaixo:

Esse é o caso geral, substituindo os valores relativos ao nosso problema:

Vamos ter:

Agora é só resolver essa equação e o valor de é a distância até a linha neutra.

Aplicando bhaskara:

Como o valor deve ser positivo

Voltando ao cálculo do momento de inércia:

Observe que aqui vamos considerar o corpor rotacionando em volta de um de seus lados, por isso o denominador .

Para a parte inferior

Somando os dois

Agora é só jogar na equação da tensão!

Observe que a distância é a maior distância entre o eixo e a peça, neste caso são iguais a e

Para o aço

Agora é só escolher o menor