Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 95
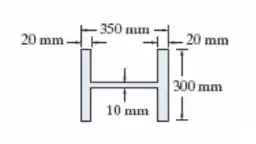
Usando as equações AISC, verifique se a coluna que tem a seção transversal mostrada na figura pode suportar uma força axial de 1.500 kN. A coluna tem comprimento de 4 m, é feita de aço A-36 e suas extremidades estão presas por pinos.
Passo 1
Falaaa, galerinha! Aqui a gente quer saber se a carga de pode ser suportada por essa coluna. Vamos usar alguns critérios de projeto das equações AISC, como ele fala e descobrir isso, belezinha?
Vamos reunir os dados que a gente tem e calcular umas coisinhas úteis sobre a nossa seção.
Como a coluna está presa por pinos nas extremidades, E temos alguns dados tabelados do aço-36:
Calculando-se o momento de inércia, teremos:
A gente calculou o momento de inércia em relação a direção . Isso porque pela seção transversal da coluna, vemos que esse momento de inércia é o menor, e é em relação ao eixo com o menor momento de inércia que a coluna tende a sofrer flambagem.
Por isso vamos usar esse cara, já que queremos saber se nossa coluna aguenta bem a carga.
Vamos calcular a área também:
Percebe que para fazer esses cálculos a gente dividiu nossa seção em 3 retângulos. Vamos seguir!
Passo 2
Podemos agora determinar o valor de Isso porque precisamos dele para saber qual fórmula usar das equações do AISC
Como temos uma coluna de aço, a gente também precisa do limite do índice de esbeltez, dado por
E a gente também precisa calcular o próprie índice de esbeltez dado por
Passo 3
Como o índice de esbeltez é menor que o limite dele, ou seja
Vamos usar essa fórmula de projeto:
A gente vai usar ela para saber se a carga admissível é menor do que . A tensão admissível pode ser escrita como
Substituindo isso na nossa fórmulinha AISC
Substituindo nossos valores e isolando
Logo, essa é a carga admissível. Como ela é maior que a carga de , a coluna vai aguentar bem a carga de .