Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 111
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine a tensão normal máxima provocada pelo momento fletor.
Passo 1
Beleza! A primeira coisa que vamos fazer é desenhar o diagrama de corpo livre para a viga, dessa forma, o DCL será:
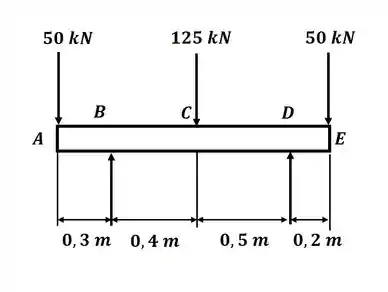
Com o DCL acima, podemos aplicar o somatório de momentos em relação ao ponto D e com isso encontrar a reação no ponto B. Então teremos:
Agora, para descobrir a reação em D, podemos aplicar o somatório de forças na direção , onde teremos:
Agora podemos escrever a equação para a força cortante, já que temos todas as forças aplicadas e os pontos onde são aplicadas. Sendo assim, considerando a origem no ponto A, com , a equação para a força cortante será:
Passo 2
Agora, para encontrarmos a equação do momento fletor, como já temos a equação para a força cortante, basta lembrar que a derivada do momento equivale a força cortante, ou seja:
Isolando as variáveis dessa equação, temos:
Integrando essa expressão dos dois lados, teremos:
Agora, substituindo a expressão encontrada para no passo 1, a equação acima se torna:
Resolvendo a integral, teremos:
Em que é a constante de integração. Nesse caso, a constante de integração corresponde aos momentos localizados que são aplicados ao sistema, no nosso, como não temos nenhum momento localizado, então teremos:
Então a equação do momento será:
Passo 3
Agora para a letra (b), para encontrar a tensão normal máxima, precisamos primeiro do momento máximo. Como só temos forças localizadas aplicadas ao sistema, sabemos que o momento máximo estará localizado sob um dos pontos de aplicação das forças. Então vamos calcular o momento nos 5 pontos da viga. Começando por A em teremos:
Agora para o ponto B em , teremos:
Agora para o ponto C em , teremos:
Agora para o ponto D em , teremos:
Agora para o ponto E em , teremos:
Então o momento máximo ocorre nos pontos B e C, em ou e será:
Passo 4
Beleza! Nós sabemos que a tensão normal máxima provocada pelo momento fletor é dada por:
No nosso caso, temos uma viga I 1150 X 18, então vamos ter que recorrer ao apêndice C para pegar suas propriedades. Precisamos do momento de inércia e da altura da viga, já que a distância para obter a tensão máxima será metade da altura da viga, pois as maiores tensões estarão na extremidade. No apêndice C temos o modelo 1150 x 18,6, vamos pegar os valores referentes a essa viga, então teremos:
Dessa forma, substituindo os valores conhecidos, nossa tensão máxima será dada por: