Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 187
Usando a equação (4.66), determine a expressão para R dada na Fig. 4.61 para uma seção transversal circular.
Passo 1
Tá legal! A primeira coisa que devemos fazer nesse exercício é esboçar a região de interesse e o elemento infinitesimal que iremos utilizar para integrar na equação 4.66, sendo assim, teremos:
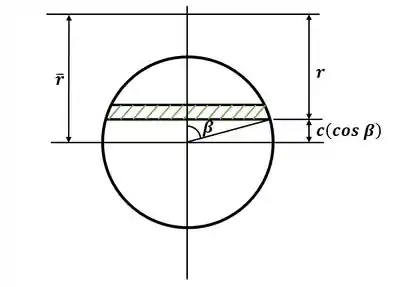
Beleza! Da figura acima, conseguimos escrever a largura da seção hachurada em função do raio e do ângulo :
Agora vamos escrever o raio da seção hachurada, que será dado por:
Derivando essa expressão dos dois lados para poder encontrar dr, chegamos em:
Agora então, podemos escrever a área da seção hachurada na forma diferencial, dada por:
Substituindo as expressões encontradas para e , chegamos em:
Passo 2
Agora, nós sabemos que a equação 4.66 apresentada nesse capítulo tem a seguinte forma:
Substituindo as expressões conhecidas, a equação acima se torna:
Agora, sabendo da relação trigonométrica fundamental que:
Substituindo essa expressão na equação de cima, teremos:
Agora nós vamos usar a estratégia de somar zero no numerador da integral utilizando o termo , então, fazendo isso, a equação acima se torna:
Agrupando os termos, teremos:
Passo 3
Agora nós vamos escrever os dois primeiros termos do numerador da integral em forma de produto, chegando em:
Separando em duas integrais, teremos:
Agora, resolvendo as integrais, chegaremos nas seguintes expressões para os limites de integração:
Substituindo os limites de integração, chegamos em:
Passo 4
Agora, simplificando a expressão obtida no final do passo 3, teremos:
Colocando em evidência, temos:
Agora vamos multiplicar a equação em cima e embaixo pelo conjugado do denominador, ou seja:
Estamos quase lá! Agora só falta colocar o 1/2 em evidência, para chegar na forma que queremos, fazendo isso então, temos:
Ufa! Essa é a equação que queríamos encontrar.
Resposta
Ei, a resposta está no passo a passo :)