Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 189
Usando a equação (4.66), determine a expressão para R dada na Fig. 4.61 para uma seção transversal triangular.
Passo 1
Tá legal! A primeira coisa que devemos fazer nesse exercício é esboçar a região de interesse e o elemento infinitesimal que iremos utilizar para integrar na equação 4.66, sendo assim, teremos:
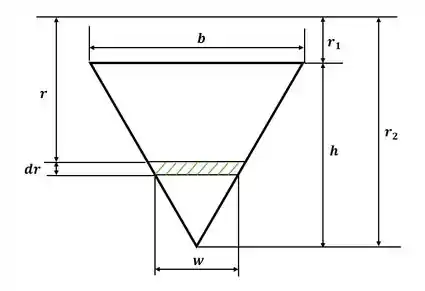
Beleza! Da figura acima, conseguimos escrever a largura da seção hachurada em função de duas constantes que vamos chamar de e e da distância do centroide.
Agora, para descobrir o valor das constantes e , vamos utilizar as condições de contorno com relação a geometria do triângulo em si, de onde teremos:
Então, substituindo essas expressões na equação para , teremos o seguinte sistema:
Isolando da segunda equação, temos:
Substituindo essa relação na primeira equação, chegamos em:
No entanto, da análise da figura, podemos ver que . Então a equação para se torna:
Passo 2
Agora vamos substituir a expressão encontrada para lá na equação para , então teremos:
E a nossa expressão para se torna:
Agora vamos escrever a expressão para a área do triângulo, que é:
E, na forma infinitesimal, temos:
Substituindo a expressão encontrada para , se torna:
Agora, nós sabemos que a equação 4.66 apresentada nesse capítulo tem a seguinte forma:
Substituindo as expressões conhecidas, a equação acima se torna:
Separando as integrais, teremos:
Passo 3
Agora vamos resolver as integrais do denominador, chegando em:
Substituindo os limites de integração, teremos:
Lembrando da figura lá do passo 1 que e colocando em evidência, chegamos em:
Finalmeeente! Conseguimos encontrar a relação que foi pedida!
Resposta
Ei, a resposta está no passo a passo :)