Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 45
Usando o método da Sec. 7.4, resolver o Prob. 7.17
Passo 1
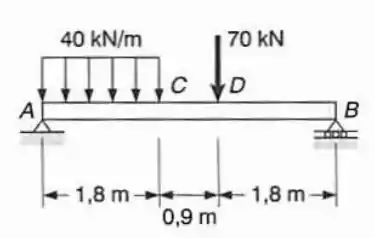
Pessoal essa questão pede para fazermos o diagrama do momento fletor e da força cortante para a viga representada. A primeira coisa que temos de fazer é achar as forças de reação em e em .
Para este exercício iremos calcular a força cortante de forma um pouco diferente, vamos escrever uma função que defina o carregamento e integrar essa função para obter a força cortante:
Depois é só derivar novamente para obter o momento fletor.
Passo 2
Vamos começar calculando as reações:
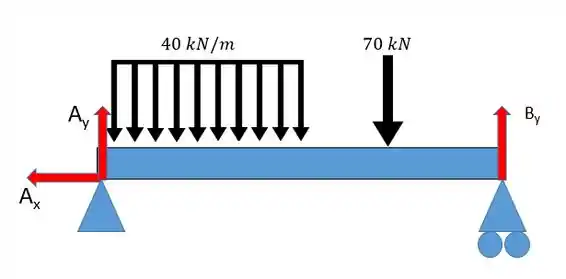
Como só existe uma força em essa força é nula, portanto . Agora podemos aplicar as equações da estática:
Repare que o termo é o valor da força relacionada à carga distribuída e é calculada como:
Voltando à equação:
Agora o momento aplicado no ponto e considerando o sentido horário positivo:
Aqui é importante perceber que a força relativa ao carregamento terá o mesmo valor do item acima e atuará na metade do comprimento do carregamento:
Substituindo:
Dessa forma:
Passo 3
Agora vamos achar a força cortante. Como falamos no primeiro passo a gente vai integrar a função que define o carregamento. Como é um carregamento uniforme vamos ter:
É uma constate!
Para calcular a força cortante:
Beleza, mas quem é ? Essa constante de integração é igual às forças que pontuais que atuam na barra. Mas repara que isso que estamos fazendo nesse passo vale apenas para . Então é igual à força atuante em :
Dessa forma, para o trecho vamos ter que a força cortante vale:
Uhulll!!
Mas faltam os trechos e , correto?
Passo 4
Vamos analisar o trecho :
Como já passamos por todo o carregamento distribuído podemos considerar ele todo como uma constante, porque o valor que esse carregamento exerce sobre a força cortante não vai mais mudar então vamos ter:
Reparem que a gente pegou o valor referente ao ponto . Como não existe nenhuma força até o ponto () esse valor permanecerá constante, logo:
Quando a gente chega em temos de subtrair o valor de já que essa força causa uma diminuição na força cortante, então teremos:
Para o trecho
E finalmente no ponto a cortante volta a ser zero, porque se soma à força em :
A gente pode desenhar o diagrama e obter uma figura assim:
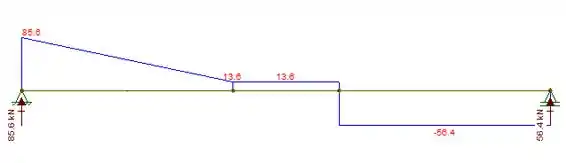
Observe que o valor máximo do momento fletor ocorre exatamente no ponto !
Passo 5
Agora vamos partir para o momento fletor a gente não precisa fazer as seções novamente só precisamos integrar os valores:
Para o trecho :
Pessoal o termo aqui vale quando temos um momento puro o que não existe na nossa viga então podemos desconsiderar esse termo em todos os trechos obtendo:
No ponto vamos ter:
Para o trecho :
No ponto vamos ter:
Para o trecho :
Pessoal a gente nem precisaria calcular no ponto porque sempre nos pontos de apoio o momento fletor né nulo!
Logo, ao fazermos o diagrama obtemos:
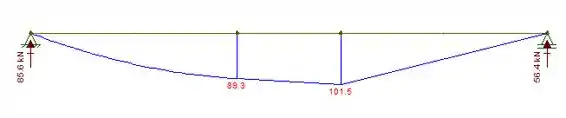
O ponto máximo ocorre no ponto e vale:
Resposta
a)
b)