Sabendo-se que e , selecionar o perfil de abas largas que poderia ser usado para suportar o carregamento mostrado.

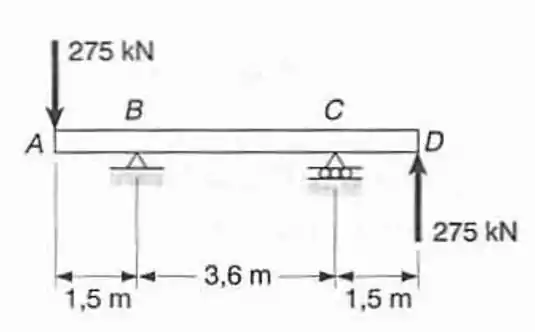
Para facilitar fazer um desenho das forças:

Nesse exercício as forças verticais vão se anular então a gente precisa fazer o momento em algum ponto, o mais lógico é o ponto B.

Não há forças na horizontal. Logo

Como as forças de se anulam, resta que:

Nós queremos o máximo momento fletor máximo e a força cortante máxima. A força cortante máxima ocorre nas extremidades e é igual ao próprio carregamento da força pontual:

Agora podemos achar o valor do momento fletor, que ocorre nos pontos de apoio:

Agora vamos achar o momento resistente mínimo que a viga deve possuir , que é dado por:

Agora vamos para a nossa tabela e vamos escolher a viga com e a mais econômica. Aqui econômica significa a viga com a menor altura nominal, logo a nossa selecionada é a seção:

Agora vamos ver se essa seção suporta a tensão de cisalhamento, utilizando a aproximação para perfis de aba larga:

A área da alma pode ser calculada como:

Substituindo o valor do cortante máximo, que já foi calculado, e os valores e que estão todos na tabela vamos ter:

Como essa tensão é menor do que a tensão admissível () então nossa viga também passou neste teste.

Agora só falta mais um último teste, que é analisar a tensão normal no ponto logo abaixo da aba. Vamos fazer isso utilizando o e a distância entre a linha neutra e esse ponto no “sovaquinho” da aba:

Sendo que a distância é calculada como:

Onde é a altura do perfil e a altura da aba. Portanto, tirando esses valores da tabela:

Substituindo os valores na equação:

Novamente o valor se mostrou inferior à nossa tensão admissível .