Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 33

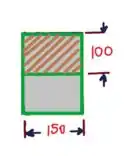
A viga em balanço AB tem uma seção transversal retangular de 150   m m   ×   200   m m . Sabendo que a força de tração no cabo BD é de 10,40   k N e desprezando o peso da viga ,determine as tensões normal e de cisalhamento nos três pontos indicados.

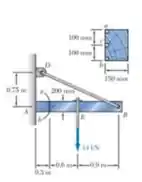
Passo 1

Muito bem gurizada, vamos começar nossos cálculos? Primeiramente vamos esboçar o diagrama de corpo livre, vem comigo :D

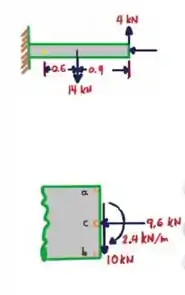
Passo 2

Dando continuidade temos:

D B _ = 0,75 2 2 + 1,8 2 2 = 1,95   m

Componente vertical de T D B : 0,75 1,95 ( 10,4 ) = 4   k N

Componente horizontal de T D B :

1,8 1,95 ( 10,4 ) = 9,6   k N

Na seção que contém os pontos a, b e c:

P = - 9,6   k N V = 14 - 4 = 10   k N

M = ( 1,5 ) ( 4 ) - ( 0,6 ) ( 14 ) = 2,4   k N / m

Passo 3

Propriedades da seção:

A = ( 0,150 ) ( 0,200 ) = 0,030   m 2

I = 1 12 ( 0,150 ) ( 0,200 ) 2 = 100 × 10 - 6   m 2

c = 0,100   m

No ponto a:

σ x = - P A - M C I =   - 9,6 × 10 3 0,030 + ( 2,4 × 10 3 ) ( 0,100 ) 100 × 10 - 6 = 2,08   M P a

σ x = 2,08   M P a

No ponto b:

σ x = - P A - M C I = - 9,6 × 10 3 0,030 - ( 2,4 × 10 3 ) ( 0,100 ) 100 × 10 - 6 = - 2,72   M P a

σ x = - 2,72   M P a

Passo 4

No ponto c:

σ x = - P A = - 9,6 × 10 3 0,030 =   - 0.320     M P a

σ x = - 0.320     M P a

Q = ( 150 ) ( 100 ) ( 50 ) = 750 × 10 3   m m 3 = 750 × 10 - 6   m 3

τ x y = - V Q I t = - ( 10 × 10 - 3 ) ( 750 × 10 - 6 ) 100 × 10 - 6 ( 150 ) =   - 0,500   M P a

τ x y = - 0,500   M P a

Resposta

  1. 2,08   M P a
  2. - 2,72   M P a
  3. - 0,500   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força vertical P age na parte inferior da capa cujo peso é desprezível. Determine a distância máxima d até a borda na qual aquela força pode ser aplicada de modo a não produzir nenhuma tensão de com