Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 81b
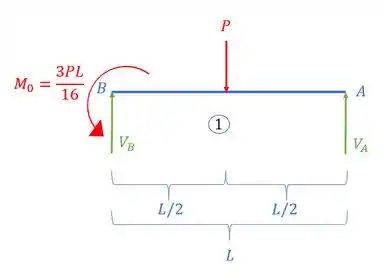
Para a viga com o carregamento mostrado, determinar a reação de apoio móvel.
Obs: determinação dos valores da viga no estado isostático para o caso 2
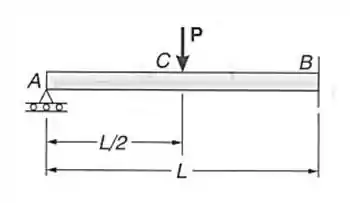
Passo 1
Como já determinamos os dados da viga 1 na parte 1, vamos agora para a vaga 2 . Como a nossa viga 2 é isostática, podemos determinar as suas reações de apoio.
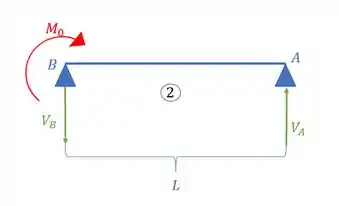
Agora perceba o seguinte, suponha que ao invés de termos os apoios em A e B, vamos supor que eles são cargas aplicadas na nossa viga, e que no caso no ponto A temos um engaste, então basta desenharmos o diagrama de cada carga com relação ao ponto A, assim, teremos que:
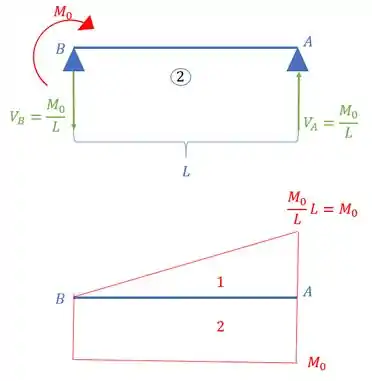
E sabemos que devemos dividir o nosso diagrama por referente a cada uma das barras, e assim teremos que:
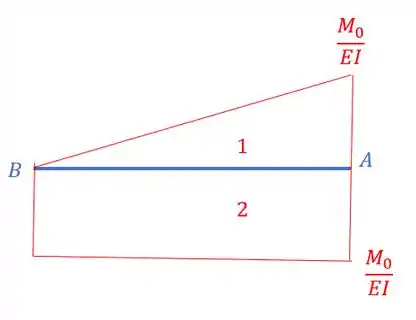
Passo 2
Agora, pensa no seguinte, como eu disse, quando tínhamos cargas simétricas, poderíamos considerar um ponto em que sabíamos que a deflexão era zero, porém, agora não sabemos mais onde temos essa deflexão, vamos partir direto para o que sabemos, que nesse caso é a deformação, e como a deformação vai nos ajudar a determinar a declividade? Muito simples, podemos determinar a deformação de A com relação a B da seguinte maneira:
E pensa no seguinte, queremos saber quanto vale o ângulo em B, certo? Vamos isolar o ângulo:
E se multiplicarmos tudo por L, obtemos exatamente as deformações, mas perceba que a do ângulo B eu não irei modificar.
E sabemos que a deformação em A é zero, assim temos que:
E para determinarmos a deformação precisamos de todas as áreas entre A e B e das distâncias desses centroides ATÉ A, bem importante lembrar que sempre determinamos a distância com relação ao primeiro termo do subscrito . Dividindo o nosso diagrama em áreas mais simples temos que:
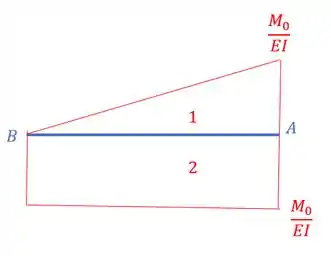
E além das áreas precisamos da distância de cada centroide até o nosso ponto A, assim teremos que:
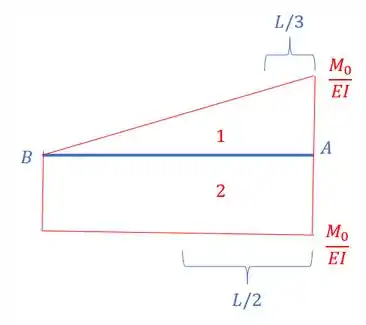
Assim podemos definir que:
Mas lembre-se que o objetivo é o ângulo, com isso teremos que:
Passo 3
Sabemos pelo item a) que o valor do ângulo no ponto B pela carga na viga 1 é dado por:
E pelo item b) sabemos que o valor do ângulo em A devido a carga da viga 2 é dado por:
E sabemos que a soma dessas cargas deve ser zero, assim temos que:
Assim o momento fletor é dado por:
Assim se olharmos a nossa viga hiperestática, teremos que como o momento deu negativo, basta aplicar ela na nossa viga com o sentido contrário:
