Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 70
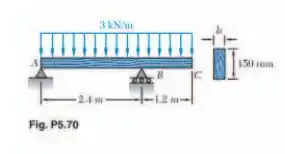
Para a viga e o carregamento mostrados na figura, projete a seção transversal da viga sabendo que o tipo de madeira utilizada tem uma tensão normal admissível de
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora fazer mais questão desse livro.
Primeiramente, sabemos que a tensão normal é dada por:
Onde é a distância da linha neutra e é o momento de inércia. Logo:
Logo, precisamos fazer o diagrama de momento para encontrar o maior momento atuante na viga e substituí-lo na forma, igualando à tensão admissível fornecida. Assim, poderemos substituir os valores e encontrar o valor de
Primeiro, precisaremos das reações. O DCL será:
Aplicando a equação de equilíbrio:
Passo 2
Agora, basta traçar o diagrama de momento:
Podemos ver que o momento máximo é Logo:
Portanto:
Pronto, seção dimensionada. Bora matar esse livro.