Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 11

A viga é composta por duas hastes e está sujeita à carga concentrada P . Determine a inclinação em C . Os momentos de inércia das hastes são I A B e I B C e o módulo de elasticidade é E .

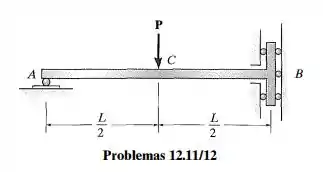
Passo 1

Para 0 ≤ x 1 ≤ L / 2 :

∑ M = 0 M x 1 - P x 1   = 0 M x 1 = P x 1

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = P x 1

E I d v 1 d x 1 = P 2 x 1 2 +   C 1

E I v 1 = P 6 x 1 3 + C 1 x 1 + C 2

Para 0 ≤ x 2 ≤ L :

∑ M = 0 M x 2 - P x 2 + P x 2 - L 2 = 0 M x 2 = P L 2

Logo:

E I d 2 v 2 d x 2 2 = P L 2

E I d v 2 d x 2 = P L 2 x 2 + C 3

E I v 2 = P L 4 x 2 2 + C 3 x 2 + C 4

Passo 2

As condições de contorno serão:

x 1 = 0 → v 1 = 0

x 2 = L → d v 2 d x 2 = 0

Já as condições de continuidade serão:

x 1 = x 2 = L 2 → v 1 = v 2   e     d v 1 d x 1 = d v 2 d x 2

Logo, substituindo:

C 1 = - 3 P L 2 8 ; C 2 = 0 ; C 3 = - P L 2 2 ; C 4 = - P L 3 48

Passo 3

Logo, a inclinação em A ocorre em x 1 = 0 :

θ A = - 3 P l 2 8 E I E a deflexão em C, ocorre em x 1 = L 2 :

v c = - P L 3 6 E I

Resposta

θ A = - 3 P l 2 8 E I

v c = - P L 3 6 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

( a ) Usando funções de singularidade, escreva as equações definindo a força cortante e o momento fletor para a viga e o carregamento mostrados. ( b ) Use a equação obtida para M para determinar o mom
Resolva o problema 5,94 considerando que a força P concentrada de 6k N aplicada a cada viga for substituída por forças concentradas P 1 e P 2 de 3k N aplicadas a uma distância de 4m de cada extremidad
( a ) Usando funções de singularidade, escreva as equações definindo a força cortante e o momento fletor para a viga e o carregamento mostrados. ( b ) Use a equação obtida para M para determinar o mom
( a ) Usando funções de singularidade, escreva as equações definindo a força cortante e o momento fletor para a viga e o carregamento mostrados. ( b ) Use a equação obtida para M para determinar o mom
( a ) Usando funções de singularidade, escreva as equações definindo a força cortante e o momento fletor para a viga e o carregamento mostrados. ( b ) Use a equação obtida para M para determinar o mom