Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 87

A viga consiste em três segmentos conectados por pinos em B e E. Determine os diagramas de força cortante e de momento fletor para a viga.

Passo 1

Oi, tudo bem? Vamos analisar esta questão.

O exercício nos pede para determinar os diagramas de força cortante e de momento fletor para a viga em questão. Vamos aprender a construir estes diagramas.

Como o sistema é composto por 3 vigas ligadas por pinos, podemos analisar cada uma separadamente.

Analisando E F , temos que:

∑ M E = 0

N F 4 - 9 4 2 = 0

N F = 18   k N

E:

∑ M F = 0

9 4 2 - E F 4 = 0

E F = 18   k N

Passo 2

Vamos realizar o mesmo procedimento para o seguimento A B . Temos que:

∑ M A = 0

B y 4,5 - 1 2 9 4,5 3 = 0

B y = 13,5   k N

E:

∑ M B = 0

1 2 9 4,5 1,5 - A y 4,5 = 0

A y = 6,75   k N

Passo 3

Analisando o membro B C D E , temos que:

∑ M C = 0

N D 2 + 13,5 2 - 9 6 1 - 18 4 = 0

N D = 49,5   k N

E:

∑ M D = 0

9 6 1 + 13,5 4 - 18 2 - N C 2 = 0

N C = 36   k N

Como descobrimos todas as reações externas, podemos construir nossas equações para avaliar os pontos e montar os diagramas.

Temos que:

6,75 - 1 2 2 x x - V = 0

V = 6,75 - x 2

Fazendo V = 0 , temos que:

x = 6,75   m

Para o momento, temos que:

M + 1 2 2 x x x 3 - 6,75 x = 0

M = 6,75 x - 1 3 x 3

O momento máximo será:

M m á x = 6,75 6,75 - 1 3 6,75 3

M M á x = 11,7   k N ⋅ m

Passo 4

Agora é só construir os diagramas com os valores em cada ponto.

Os diagramas de força cortante e momento fletor ficam, respectivamente, assim:

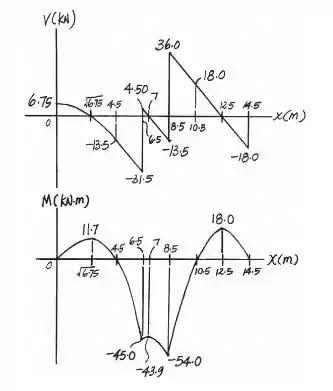
Resposta

Os diagramas de força cortante e momento fletor ficam, respectivamente, assim:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a maior intensidade w 0 da carga distribuída que a viga pode suportar se a viga suporta uma força cortante máxima V m á x = 6k N á e um momento fletor máximo M m á x = 1k N ∙ m á .
Determine os diagramas de esforço cortante e de momento fletor para a viga com extremidade em balanço.
Determine os diagramas de esforço cortante e de momento fletor para a viga C D .
Determine a maior intensidade w 0 da carga distribuída que a viga pode suportar se a viga suporta um momento fletor máximo M m á x = 20k N ∙ m á e uma força cortante máxima V m á x = 80k N á .
O eixo falhará quando o momento fletor máximo for M m á x = 50k N ∙ m á ou o esforço cortante máximo for V m á x = 40k N á . Determine a maior intensidade w da carga distribuída que a viga