Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 45
Se , viga falhará quando a força cortante máxima for ou o momento fletor máximo . Determine o maior momento binário que a viga suportará.
Passo 1
O problema quer que a gente determine maior momento binário que a viga suporta antes de falhar, ou seja, quando o ou o .
Para isso, vamos começar pensando um pouco sobre o que temos e fazer um diagrama de corpo livre que ficará assim:
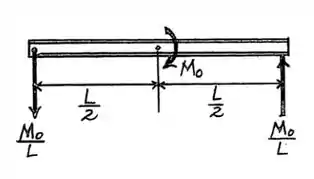
Passo 2
Então agora, vamos calcular o esforço contante e o momento fletor genérico na região .
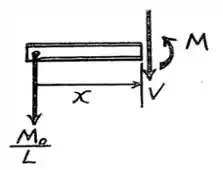
Para isso, vamos levar lembrar que a viga tá em equilíbrio assim:
Assim, encontramos que:
E se pegamos o somatório dos momentos:
Então, agora vamos fazer o mesmo na região .
Assim encontramos o esforço e o momento de forma genérica, sem dar uma valor para o .
Que são:
Passo 3
Então agora sim, que já sabemos tudo isso, calculamos o binário máximo, vamos começar calculando o esforço cortante máximo:
Logo:
Agora, vamos para o momento:
Então como é o máximo, nós pegamos o menor, que é